How to Find Complementary and Supplementary Angles? (+FREE Worksheet!)

In this article, we will introduce you to the rules of complementary and supplementary angles and how to use them to find the value of a missing angle.
Related Topics
- Special Right Triangles
- How to Solve Triangles Problems
- How to Find Volume and Surface Area of Cubes
- How to Calculate Cylinder Volume and Surface Area
- How to Solve Parallel Lines and Transversals Problems
Definition of the Complementary and supplementary angles
- Two angles with a sum of 90 degrees are called complementary angles.
- Two angles with a sum of 180 degrees are Supplementary angles.
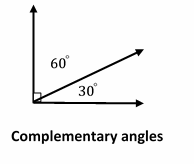
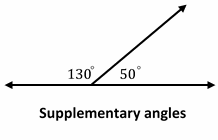
Examples
Complementary and supplementary angles – Example 1:
Find the missing angle.
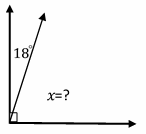
Solution:
Notice that the two angles form a right angle. This means that the angles are complementary, and their sum is 90.
Then: \(18+x=90→x=90^\circ-18^\circ=72^\circ\) The missing angle is 72 degrees
Complementary and supplementary angles – Example 2:
Angles Q and S are supplementary. What is the measure of angle Q if angle S is 35 degrees?
Solution:
Q and S are supplementary \(→Q+S=180→Q+35=180→ Q =180-35=145\)
Complementary and supplementary angles – Example 3:
Find the missing angle.
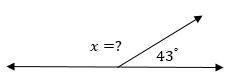
Solution:
Notice that two angles form a straight angle when together. This means that the angles are supplementary and have a sum of \(180^\circ\).
\(x+43=180→x=180-43=137^\circ\)
Complementary and supplementary angles – Example 4:
Find the missing angle.
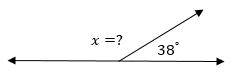
Solution:
Notice that two angles form a straight angle when together. This means that the angles are supplementary and have a sum of \(180^\circ\).
\(x+38=180→x=180-38=142^\circ\)
Exercises for Complementary and supplementary angles
Find the missing measurement in the pair of angles.
Find the missing measurement in the pair of angles.
1. \(\color{blue}{x=}\)
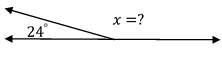
2.\(\color{blue}{x=}\)
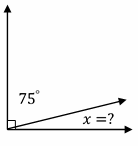
3.\(\color{blue}{x=}\)
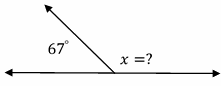
4.\(\color{blue}{x=}\)
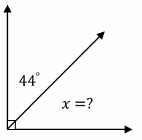
5.The measure of an angle is \(31^°\). What is the measure of its complementary angle? __________
6.The measure of an angle is \(76^°\). What is the measure of its supplementary angle? __________

- \(\color{blue}{156^\circ}\)
- \(\color{blue}{15^\circ}\)
- \(\color{blue}{113^\circ}\)
- \(\color{blue}{46^\circ}\)
- \(\color{blue}{59^\circ}\)
- \(\color{blue}{104^\circ}\)
Related to This Article
More math articles
- What Kind of Math Is Taught in 8th Grade?
- How to Master the World of Conjectures and Counterexamples
- The Ultimate 6th Grade MAP Math Course (+FREE Worksheets)
- How to Find The Slope of Roots: Derivative of Radicals
- ACCUPLACER Math – Test Day Tips
- Best Blue Light Glasses for Teachers and Students
- Your Coach’s Playbook: How to Understand Percent of Change
- 10 Most Common 8th Grade Georgia Milestones Assessment System Math Questions
- 5 Best Praxis Core Math Study Guides
- How to Calculate the Volume of Cubes and Prisms





























What people say about "How to Find Complementary and Supplementary Angles? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.