How to Find the Volume of Cones and Pyramids? (+FREE Worksheet!)

Related Topics

• How to Solve Pythagorean Theorem Problems
• How to Solve Triangles Problems
• How to Find the Perimeter of Polygons
• How to Calculate the Area of Trapezoids

Step by step guide to Find Volume of Cones and Pyramids

A cone is a three-dimensional geometric figure that has a flat surface and a curved surface pointed towards the top point called the vertex.  In other words, the geometric shape of the cone is limited to its base plate and consists of joining straight lines that connect the top of the cone to the points around the base.

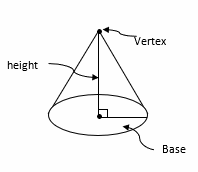
To get the volume of the cone, we have to calculate the area of the base surface (circle) and multiply it by the height. Then divide the resulting value by \(3\) to get the volume of the cone. Therefore, the formula for calculating the volume of a cone is as follows:

Volume of Cones: \(\frac{1}{3}\)\(\times\)area of base\(\times\)height

This relation based on mathematical symbols will be as follows:

\(V=\frac{1}{3}\times B\times h=\frac{1}{3}πr^2h\)

Note that in the above relation, \(V\) is the symbol of volume, \(r\) and \(h\) represent the radius of the cone and its height.

A pyramid is a three-dimensional geometric figure that has a polygon base and triangular faces pointed towards the top point called the vertex. The height of a pyramid is a line that is from the top of the pyramid to its base and is perpendicular to the surface of the base.

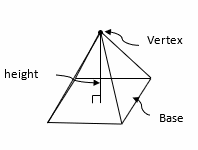
To calculate the volume of a pyramid, we must first find the area of the base surface and then multiply it by its height. Divide the resulting value by 3 and finally, the volume of the pyramid is obtained. Therefore, the formula for calculating the volume of the pyramid will be as follows:

Volume of a pyramid: \(\frac{1}{3}\)\(\times\)area of base\(\times\)height

The above formula is based on mathematical symbols as follows:

\(V=\frac{1}{3}\times B\times h\)

Note that the above formula \(V\) symbolizes the volume of the pyramid, \(b\) is the area of the base surface and \(h\) is the height of the pyramid.

Finding Volume of Cones and Pyramids – Example 1:

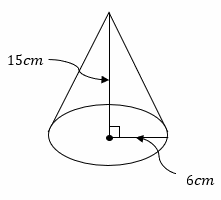
Find the volume of the following cone. \((π=3.14)\)

Solution:

Use the formula for the volume of cones\(=\frac{1}{3}πr^2h\)

Substitute \(6\) for \(r\) and \(15\) for \(h\) :

\(=\frac{1}{3}πr^2h=\)\(\frac{1}{3} \times 3.14 \times (6)^2 \times (15)=565.2 {cm}^3\)

Finding Volume of Cones and Pyramids – Example 2:

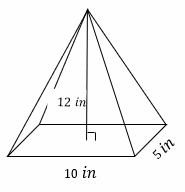
Find the volume of the pyramid.

Solution:

The volume of a pyramid\(=\frac{1}{3}\times B\times h\)  

\(B=10\times 5=50\)  

Substitute \(50\) for \(B\) and \(12\) for \(h\):

\(=\frac{1}{3}\times B\times h=\frac{1}{3}\times 50\times 12=200 {in}^3\)

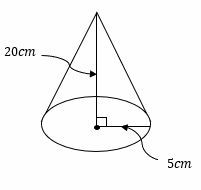
Finding Volume of Cones and Pyramids – Example 3:

Find the volume of the following cone. \((π=3.14)\)

Solution:

Use the formula for the volume of cones\(=\frac{1}{3}πr^2h\)

Substitute \(5\) for \(r\) and \(20\) for \(h\):

\(=\frac{1}{3}πr^2h=\)\(\frac{1}{3} \times 3.14 \times (5)^2 \times (20)=523.33 {cm}^3\)

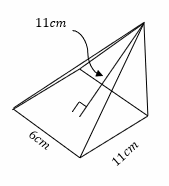
Finding Volume of Cones and Pyramids – Example 4:

Find the volume of the pyramid.

Solution:

The volume of a pyramid\(=\frac{1}{3}\times B\times h\)  

\(B=6\times 11=66\)  

Substitute \(66\) for \(B\) and \(11\) for \(h\):

\(=\frac{1}{3}\times B\times h=\frac{1}{3}\times 66\times 11=242 {cm}^3\)

Exercises for Finding Volume of Cones and Pyramids

Find the volume of each figure.\((π=3.14)\)

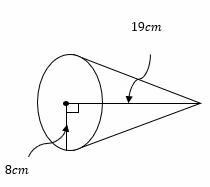
2.

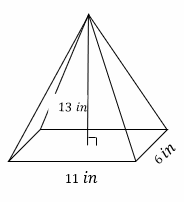
3.

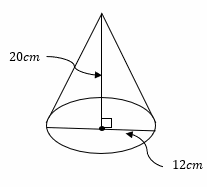
4.

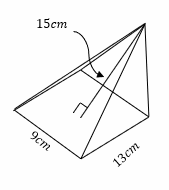
1. \(\color{blue}{V≈1,272 {cm}^3}\)
2. \(\color{blue}{V=286 {in}^3}\)
3. \(\color{blue}{V≈3,014 {cm}^3}\)
4. \(\color{blue}{V=585 {cm}^3}\)