6th Grade IAR Math Practice Test Questions
Do you need practice resources to better prepare your 6th-grade student for the IAR math test? Look no further because we give you what you need! Using the common questions of the Illinois Assessment of Readiness (IAR) math test, you can measure the readiness of 6th-grade students.
These are skill-building questions designed to meet the exact needs of the 6th-grade student. There is also a step-by-step guide to solving 10 common math problems at the end of the section.
The Absolute Best Book to Ace the IAR Math Test
10 Sample 6th Grade IAR Math Practice Questions
1- What is the missing prime factor of a number \(420\)?
\(420=2^2×3^1×…\)
A. \(2^2×3^1×5^1×7^1\)
B. \(2^2×3^1×7^1×9^1\)
C. \(1^2×2^3×2^1×3^1\)
D. \(3^2×5^1×7^1×9^1\)
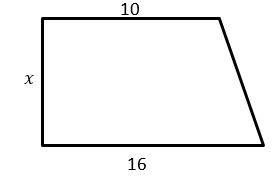
2- If the area of the following trapezoid is equal to \(A\), which equation represents \(x\)?
A. \( x = \frac{13}{A}\)
B. \( x = \frac{A}{13}\)
C. \( x=A+13\)
D. \( x=A-13\)
3- By what factor did the number below change from the first to the fourth number?
\(8, 104, 1352, 17576\)
A. \(13\)
B. \(96\)
C. \(1456\)
D. \(17568\)
4- \(170\) is equal to …
A. \( -20-(3×10)+(6×40)\)
B. \(((\frac{15}{8})×72 )+ (\frac{125}{5}) \)
C. \(((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4}\)
D. \(\frac{481}{6} + \frac{121}{3}+50\)
5- The distance between the two cities is \(3,768\) feet. What is the distance between the two cities in yards?
A. \(1,256 yd\)
B. \(11,304 yd\)
C. \(45,216 yd\)
D. \(3,768 yd\)
6- Mr. Jones saves \($3,400\) out of his monthly family income of \($74,800\). What fractional part of his income does Mr. Jones save?
A. \(\frac{1}{22}\)
B. \(\frac{1}{11}\)
C. \(\frac{3}{25}\)
D. \(\frac{2}{15}\)
7- What is the lowest common multiple of \(12\) and \(20\)?
A. \(60\)
B. \(40\)
C. \(20\)
D. \(12\)
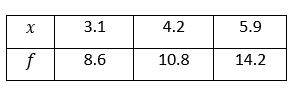
8- Based on the table below, which expression represents any value of \(f\) in terms of its corresponding value of \(x\)?
A. \(f=2x-\frac{3}{10}\)
B. \(f=x+\frac{3}{10}\)
C. \(f=2x+2 \frac{2}{5}\)
D. \(2x+\frac{3}{10}\)
9- \(96 kg\) \(=\)… ?
A. \(96 mg\)
B. \(9,600 mg\)
C. \(960,000 mg\)
D. \(96,000,000 mg\)
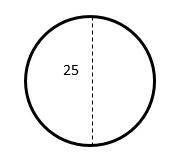
10- Calculate the approximate area of the following circle. (the diameter is \(25\))
A. \(78\)
B. \(491\)
C. \(157\)
D. \(1963\)
Best 6th Grade IAR Math Prep Resource
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Answers:
1- A
\(420=2^2×3^1×5^1×7^1\)
2- B
The area of the trapezoid is: area= \(\frac{(base 1+base 2)}{2})×height= ((\frac{10 + 16}{2})x = A\)
\( →13x = A→x = \frac{A}{13}\)
3- A
\(\frac{104}{8}=13, \frac{1352}{104}=13, \frac{17576}{1352}=13\)
Therefore, the factor is \(13\).
4- C
Simplify each option provided.
\( A. -20-(3×10)+(6×40)=-20-30+240=190\)
\( B. (\frac{15}{8})×72 + (\frac{125}{5}) =135+25=160\)
\(C. ((\frac{30}{4} + \frac{15}{2})×8) – \frac{11}{2} + \frac{222}{4} = ((\frac{30 + 30}{4})×8)- \frac{11}{2}+ \frac{111}{2}=(\frac{60}{4})×8) + \frac{100}{2}= 120 + 50 = 170\)
this is the answer
\(D. \frac{481}{6} + \frac{121}{3}+50= \frac{481+242}{6}+50=120.5+50=170.5\)
5- A
\(1\) \(yard\) \(= \)\(3 feet\)
Therefore, \(3,768 ft × \frac{1 \space yd }{3 \space ft}=1,256 \space yd\)
6- A
\(3,400\) out of \(74,800\) equals to \(\frac{3,400}{74,800}=\frac{17}{374}=\frac{1}{22}\)
7- A
Prime factorizing of \(20=2×2×5\)
Prime factorizing of \(12=2×2×3\)
\(LCM\)\(=2×2×3×5=60\)
8- C
Plug in the value of \(x\) into the function \(f\). First, plug in \(3.1\) for \(x\).
\(A. f=2x-\frac{3}{10}=2(3.1)-\frac{3}{10}=5.9≠8.6\)
\(B. f=x+\frac{3}{10}=3.1+\frac{3}{10}=3.4≠10.8\)
\(C. f=2x+2 \frac{2}{5}=2(3.1)+2 \frac{2}{5}=6.2+2.4=8.6 \)
This is correct!
Plug in other values of \(x. x=4.2\)
\(f=2x+2\frac{2}{5} =2(4.2)+2.4=10.8 \)
This one is also correct.
\(x=5.9\)
\(f=2x+2 \frac{2}{5}=2(5.9)+2.4=14.2 \)
This one works too!
\(D. 2x+\frac{3}{10}=2(3.1)+\frac{3}{10}=6.5≠8.6\)
9- D
\(1 kg\)\(=\) \(1000 g\) and \(1 g\) \(=\) \(1000 mg\)
\(96 kg\)\(=\) \(96\) \(×\) \(1000 g\) \(=\)\(96\) \(×\) \(1000 \)\(×\) \(1000\) \(=\)\(96,000,000 mg\)
10- B
The diameter of a circle is twice the radius. Radius of the circle is \(\frac{25}{2}\).
Area of a circle = \(πr^2=π(\frac{25}{2})^2=156.25π=156.25×3.14=490.625≅491\)
Looking for the best resource to help you succeed on the 6th Grade IAR Math test?
The Most Comprehensive Review for 6th-Grade Students
Common Core Math Exercise Book for Grade 6 Student Workbook and Two Realistic Common Core Math Tests
Related to This Article
More math articles
- How to Solve Logarithmic Equations: Definition and Properties
- Top Proven Strategies To Increase Your SAT Math Score
- FREE 5th Grade STAAR Math Practice Test
- Top 10 ATI TEAS 7 Prep Books (Our 2023 Favorite Picks)
- The Best Calculators for Grade 9 Students
- Which Test Is Better for You; GED, TASC, or HiSET? Find Out Now
- 7th Grade MEAP Math FREE Sample Practice Questions
- How to Use Partial Products to Multiply One-Digit Numbers By Multi-digit Numbers
- Full-Length CLEP College Mathematics Practice Test-Answers and Explanations
- A Comprehensive Collection of Free CBEST Math Practice Tests
What people say about "6th Grade IAR Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.