Full-Length ALEKS Math Practice Test-Answers and Explanations
Did you take the ALEKS Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
ALEKS Math Practice Test Answers and Explanations
1- The answer is 38
\($7×8=$56\), Petrol use: \(8×1.5=12\) liters
Petrol cost: \(12×$1.5=$18\). Money earned: \($56-$18=$38\)
2- The answer is 22.016
First, multiply the tenth place of 4.3 by 5.12. The result is 1.536. Next, multiply 4 by 5.12 which results in 20.48. The sum of these two numbers is: 1.536 + 20.48 = 22.016
3- The answer is 340
Dividing 85 by \(25\%\), which is equivalent to 0.25, gives 340. Therefore, \(25\%\) of 340 is 85.
4- The answer is \(25\%\)
Use this formula: Percent of Change \(=\frac{New \space Value-Old \space Value}{Old \space Value} ×100\%\)
\(\frac{24,000-32,000}{32,000}×100\%=25\%\) and \(\frac{18,000-24,000}{24,000}×100\%=25\%\)
5- The answer is 490
Let x be the original price. If the price of the sofa is decreased by \(13\%\) to $426.3, then: \(87\%\) of \(x=426.3 ⇒ 0.87x=426.3 ⇒ x=426.3÷0.87=490\)
6- The answer is \(15\%\)
The percent of girls playing tennis is: \(30\% × 50\% = 0.30 × 0.50 = 0.15= 15 \%\)
7- The answer is \(200\%\)
Write the equation and solve for B: \(0.80 A = 0.40 B\), divide both sides by 0.40, then: \(\frac{0.80}{0.40}A=B\), therefore: \(B = 2A\), and B is 2 times of A or it’s \(200\%\) of A.
8- The answer is 6 hours and 30 minutes
Use distance formula: Distance = Rate × time ⇒ 390 = 60 × T, divide both sides by 60⇒ \(\frac{390}{60}\) = T ⇒ T = 6.5 hours. Change hours to minutes for the decimal part. 0.5 hours = 0.5 × 60 = 30 minutes.
9- The answer is \(120\%\)
Use percent formula: \(part = \frac{percent}{100}×whole\) , \(84=\frac{percent}{100}×70 ⇒ 84=\frac{percent ×70}{100} ⇒\), multiply both sides by 100 ⇒ 8400 = percent × 70, divide both sides by 70.
120 = percent
10- The answer is 6.832
To add decimal numbers, line them up and add from the right. \(1.78+3.045+2.007=6.832\)
The Absolute Best Book to Ace the ALEKS Math Test
11- The answer is 17
Use Pythagorean Theorem: \(a^2+b^2=c^2, 82 + 152 = c^2 ⇒ 64+225=c^2 ⇒ 289=c^2⇒c=17\)
12- The answer is 40
The sum of supplement angles is 180. Let \(x\) be that angle. Therefore, \(x = \frac{2}{9}×180, x = 40\)
13- The answer is 6:7
The average speed of john is: \(210÷7=30\) km
The average speed of Alice is: \(175÷5=35\) km
Write the ratio and simplify. \(30: 35 ⇒ 6: 7\)
14- The answer is $40
\($8.5×10=$85\), Petrol use: \(10×3=30\) liters, Petrol cost: \(30×$1.5=$45\)
Money earned: \($85-$45=$40\)
15- The answer is 9
Let \(x\) be the number. Write the equation and solve for \(x\).
\((45 – x) ÷ x = 4\)
Multiply both sides by \(x\).
\((45 – x) = 4x\), then add \(x\) both sides. \(45 = 5x\), now divide both sides by 5. \(x = 9\)
16- The answer is 2000
If the length of the box is 40, then the width of the box is one-fourth of it, 10, and the height of the box is 5 (one second of the width). The volume of the box is: V = lwh = (40) (10) (5) = 2000
17- The answer is 140
To find the number of possible outfit combinations, multiply the number of options for each factor: 4 × 5 × 7 = 140
18- The answer is 72
The area of the trapezoid is: \(Are=\frac{1}{2} h(b_1+b_2 )=\frac{1}{2}(x)(24+16)=300→20x=300→x=15\)⇒ \(z=\sqrt{8^2+15^2}=\sqrt{64+225}=\sqrt{289}=17\)
The perimeter of the trapezoid is: \(16+8+17+16+15=72\)
19- The answer is \(\frac{8}{25}\)
There are 25 integers from 5 to 30. Set of numbers that are not composite between 5 and 30 is: \({ 5,7,11,13,17,19,23,29}\)⇒ 8 integers are not composite. Probability of not selecting a composite number is:
\(Probability= \frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}= \frac{8}{25}\)
20- The answer is 26 miles
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem:
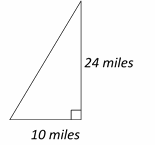
\(a^2+ b^2=c^2 , 24^2+ 10^2=c^2
⇒ 576+100= c^2 ⇒ 676=c^2 ⇒ c=26\)
Best ALEKS Math Prep Resource for 2022
21- The answers are 11 and 13.5
You can find the possible values of and b in \((ax+3)(bx-4)\) by using the given equation \(a+b=5\) and finding another equation that relates the variables a and b. Since \((ax+3)(bx-4)=-6x^2+2cx+10\), expand the left side of the equation to obtain
\(abx^2-4ax+3bx-12=-6x^2+2cx+10\)
Since ab is the coefficient of \(x^2\) on the left side of the equation and 10 is the coefficient of \(x^2\) on the right side of the equation, it must be true that \(ab=-6\)
The coefficient of \(x\) on the left side is \(3b-4a\) and the coefficient of \(x\) in the right side is \(2c\). Then: \(\frac{3b-4a}{2}=c, a+b=5\), then: \(a=5-b\)
Now, plug in the value of \(a\) in the equation \(ab=-6\). Then: \(ab=-6→(5-b)b=-6→5b-b^2=-6\)⇒ Add \(-5b+b^2\) both sides. Then: \(b^2-5b-6=0\)
Solve for \(b\) using the factoring method. \(b^2-5b-6=0→(b-6)(b+1)=0\)
Thus, either \(b=6\) and \(a =-1\), or \(b =-1\) and \(a =6\). If \(b =6\) and \(a =-1\), then
\(c=\frac{3b-4a}{2}=\frac{3(6)-4(-1)}{2}=11\). If \(b=-1\) and \(a =6\), then, \(c=\frac{3b-4a }{2}=\frac{3(-1)-4(6)}{2}=\frac{27}{2}=13.5→c=13.5\). Therefore, the two possible values for \(c\) are 11 and 13.5.
22- The answer is \(15x+2\)
If \(f(x)=7x+2(1-x)\), then find \(f(3x)\) by substituting \(3x\) for every \(x\) in the function. This gives: \(f(3x)=7(3x)+2(1-(3x))\) ⇒ It simplifies to: \(f(3x)=7(3x)+2(1-(3x))=21x+2-6x=15x+2\)
23- The answer is 17
The input value is 5. Then: \(x=-4⇒ f(x)=2x^2+4x+1→f(-4)=2(-4)^2+4(-4)+1=17\)
24- The answer is \(cosA=\frac{3}{5}\)
To solve for \(cosA\) first identify what is known.
The question states that ∆ABC is a right triangle whose \(n∠B=90\circ\) and \(sinC=\frac{3}{5}\).
It is important to recall that any triangle has a sum of interior angles that equals 180 degrees. Therefore, to calculate \(cosA\) use the complementary angles identify of a trigonometric function. \(cosA=cos(90-C)\), Then: \(cosA=sinC\)
For complementary angles, the sin of one angle is equal to the \(cos\) of the other angle. \(cosA=\frac{3}{5}\)
25- The answer is \(y=x^2-4x+1\)
To figure out what the equation of the graph is, first find the vertex. From the graph, we can determine that the vertex is at \((2,-3)\).
We can use vertex form to solve for the equation of this graph.
Recall vertex form, \(y=a(x-h)^2+k\), where h is the x coordinate of the vertex, and k is the y coordinate of the vertex. Plugging in our values, you get \(y=a(x-2)^2-3\)
To solve for a, we need to pick a point on the graph and plug it into the equation.
Let’s pick \((4,1)\), \(1=a(4-2)^2-3\), \(1=a(2)^2-3\), \(1=4a-3\), \(a=1\)⇒ Now the equation is : \(y=(x-2)^2-3\), Let’s expand this, \(y=(x^2-4x+4)-3\), \(y=x^2-4x+1\)
26- The answer is \(-\frac{2}{3}\)
Multiplying each side of \(\frac{7}{x}=\frac{21}{x+4} by x(x+4)\) gives \(7(x+4)=21x\), divide two side by 7.
\(x+4=3x\) or \(x=2\). Therefore, the value of \(-\frac{x}{3}=-\frac{2}{3}\).
27- The answer is 12
It is given that \(g(6)=8\). Therefore, to find the value of \(f(g(6))\), then \(f(g(6))=f(8)=12\)
28- The answer is \(49\sqrt{3}\)
The area of the triangle is: \(\frac{1}{2}\) AD × BC and AD is perpendicular to BC. Triangle ADC is a \(30^\circ-60^\circ- 90^\circ\) right triangle. The relationship among all sides of the right triangle \(30^\circ-60^\circ- 90^\circ\) is provided in the following triangle: In this triangle, the opposite side of the 30° angle is half of the hypotenuse. And the opposite side of \(60^\circ\) is opposite of \(30^circ × \sqrt{3}\)
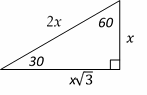
CD = 7, then AD = \(7 × \sqrt{3}\)
Area of the triangle ABC is: \(\frac{1}{2}\) AD×BC = \(\frac{1}{2}\) \(7\sqrt{3}×14=49\sqrt{3}\)
29- The answer is 40
It is given that \(g(4)=10\). Therefore, to find the value of \(f(g(4))\), substitute 10 for \(g(4)\).
\(f(g(4))=f(10)=40\).
30- The answer is \(\sqrt{17}\)
The equation of a circle with center (h, k) and radius r is \((x-h)^2+(y-k)^2=r^2\). To put the equation \(x^2+y^2-6x+4y=4\) in this form, complete the square as follows:
\(x^2+y^2-6x+4y=4, (x^2-6x)+(y^2+4y)=4\)
\((x^2-6x+9)-9+(y^2+4y+4)-4=4, (x-6)^2+(y+4)^2=17\)
Therefore, the radius of the circle is \(\sqrt{17}\)
The Best Study Guide for the ALEKS Math Test
More from Effortless Math for ALEKS Test …
Need the best online course to help you succeed on the ALEKS Math test?
Here is a complete course covering all ALEKS Math topics: The Ultimate ALEKS Math Course.
Each lesson contains notes, examples, exercises, and activities to help you learn and understand each concept easily.
Looking for FREE ALEKS Math worksheets to help you measure your exam readiness?
Here is a comprehensive and perfect collection of everything on the ALEKS Math that a test taker needs to learn before the test day: ALEKS Math Worksheets: FREE & Printable.
Don’t miss our complete list of ALEKS Math Formulas. Keep this list around for a quick reminder when you forget one of the formulas.
The Best Books to Ace the ALEKS Math Test
Have any questions about the ALEKS Test?
Write your questions about the ALEKS or any other topics below and we’ll reply!
Related to This Article
More math articles
- 4th Grade IAR Math Practice Test Questions
- How to Use Models to Divide Whole Numbers by Unit Fractions?
- 8th Grade FSA Math Worksheets: FREE & Printable
- How to Simplify Polynomials? (+FREE Worksheet!)
- FREE TABE Math Practice Test
- 5th Grade ACT Aspire Math Practice Test Questions
- How to Find Mean, Median, Mode, and Range of the Given Data? (+FREE Worksheet!)
- Full-Length Accuplacer Math Practice Test-Answers and Explanations
- Geometry Puzzle – Challenge 66
- 8th Grade NYSE Math Practice Test Questions
What people say about "Full-Length ALEKS Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.