How to Estimate Limit Values from the Graph?

Finding limits means we have to consider approximately some values of \(x\) which are closer to the given number from the left and right sides. And check for which value of \(x\) we are getting the function undefined. We can also check this with a graph.

Related Topics

• How to Define Limits Analytically Using Correct Notation
• How to Select Procedures for Determining Limits
• Properties of Limits

A step-by-step guide to Estimate limit values from the graph

When your pre-calculus teacher gives you the graph of a function and asks you to calculate the limits, you read values from the graph, something you’ve been doing since you first discovered what a graph was!

You follow that function from the left-hand side toward the \(x\) value in question if you’re seeking a limit from the left.

To find the correct limit, repeat the method from the right. If the \(y\) value approached from the left and the \(y\) value approached from the right are the same (did the pencils meet? ), then that \(y\) value is the limit.

Because graphing a function is a time-consuming and involved operation, you should only utilize it if you’ve been provided the graph.

Estimating Limit Values from the Graph – Example 1:

Find the limit of \( lim_{x\to -1}f(x)\) graphically.

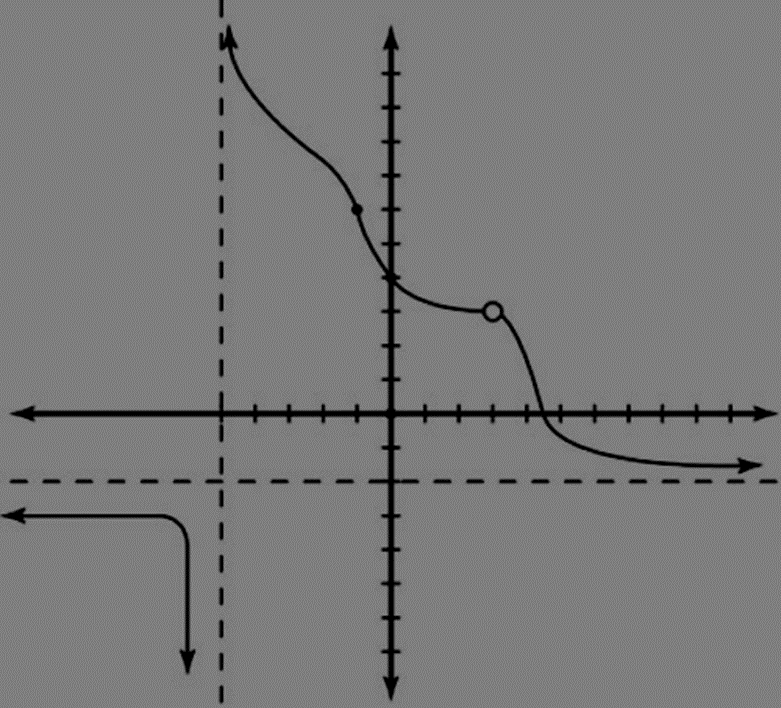
You can see that as the \(x\)-value gets closer and closer to \(–1\), the value of the function \(f(x)\) gets \(6\). And when \(x\) reaches \(–1\), the function’s value is \(6\)! However, technically, having \(f(–1) = 6\) isn’t required to say that the limit is \(6\); the function could have a hole in it at that point, and the limit would still be \(6\)!

Estimating Limit Values from the Graph – Example 2:

In the above graph, find the limit of \( lim_{x\to 3}f(x)\) graphically.

You can see a hole in the function at \(x = 3\), which means that the function is not defined – but that does not mean you can not state a limit. If you look at the values of the function from the left, \( lim_{x\to 3^-}f(x)\), and from the right, \( lim_{x\to 3^+}f(x)\), you see that the \(y\) value approaches \(3\). So you say that the limit of the function as \(x\) approaches \(3\) is \(3\).

Exercises for Estimate Limit Values from the Graph

• Find the limit of \( lim_{x\to -2}f(x)\) graphically.

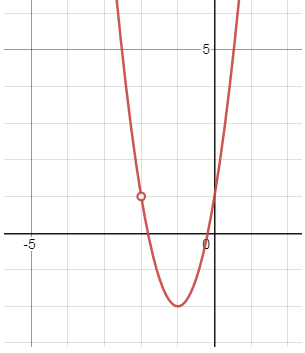
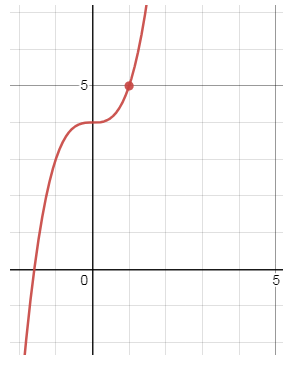
• \(\color{blue}{lim_{x\to -2}f(x)=1}\)
• \(\color{blue}{lim_{x\to 1}f(x)=5}\)