How to Define Limits Analytically Using Correct Notation?

The Limits in maths are unique real numbers. Let’s consider a function with real value \(f\) and the real number \(a\), the limit is usually defined as the \(lim_{x\to a}{f(x)}=C\). It is read as “the limit of \(f\) of \(x\), as \(x\) approaches \(a\) equals \(C\)“ . The “lim” shows the limit.

Related Topics

• How to Estimate Limit Values from the Graph
• How to Select Procedures for Determining Limits
• Properties of Limits

A step-by-step guide to defining limits analytically using correct notation

Steps for Analytically Representing Limits Using the Correct Notation:

• The first step is to figure out what value \(x\) is close to. This value will be \(a\).
• The second step is to determine the function. \(f\) is the name of the function \((x)\).
• The third step is to write the right notation for the limit analytically.

An Analytical Notation for Expressing Limits Analytically:

• A limit is an output \((y)\) value a function will approach while approaching a certain input \((x)\) value.
• When an input value approaches zero, the limit notation is used to show how close a function is to reaching its output value.

To show a limit analytically in the correct way, it should be written in this way:

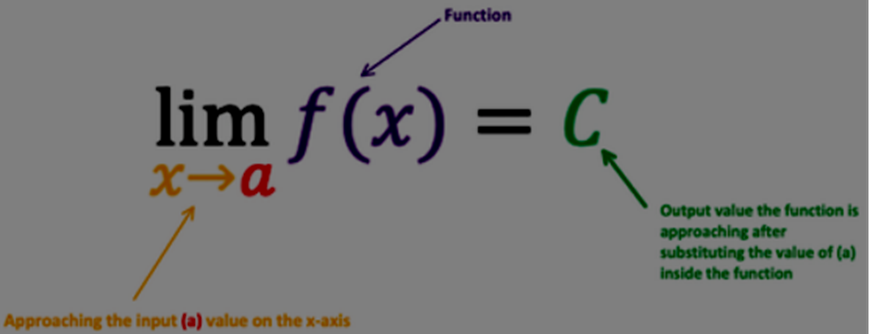
Defining Limits Analytically Using Correct Notation – Example 1:

Use correct notation to express the limit of \(f(x)=3x^2+2x-4\) as \(x\) approaches \(2\).

First, identify \(a\) value →  \(a=2\)

Then, identify \(f(x)\) →  \(f(x)=3x^2+2x-4\)

Now, write the correct notation:

\(lim_{x\to 2}{(3x^2+2x-4)}=C\)

Defining Limits Analytically Using Correct Notation – Example 2:

Use correct notation to express the limit of \(f(x)=x^4+10x+5\) as \(x\) approaches \(-3\).

First, identify \(a\) value →  \(a=-3\)

Then, identify \(f(x)\) →  \(f(x)=x^4+10x+5\)

Now, write the correct notation:

\(lim_{x\to -3}{(x^4+10x+5)}=C\)

Exercises for Defining Limits Analytically Using Correct Notation

1. Use correct notation to express the limit of \(f(x)=-3x-7x^2+20\) as \(x\) approaches \(12\).
2. Use correct notation to express the limit of \(f(x)=-6x^3-5x+11\) as \(x\) approaches \(-6\).
3. Use correct notation to express the limit of \(f(x)=5x^2+8x-3\) as \(x\) approaches \(-4\).
4. Use correct notation to express the limit of \(f(x)=25x^5+22x^2-13\) as \(x\) approaches \(5\).

1. \(\color{blue}{\lim_{x\to 12}(-3x-7x^2+20)=C}\)
2. \(\color{blue}{\lim_{x\to -6}(-6x^3-5x+11)=C}\)
3. \(\color{blue}{\lim_{x\to -4}(5x^2+8x-3)=C}\)
4. \(\color{blue}{\lim_{x\to 5}(25x^5+22x^2-13)=C}\)