Continuity at a point Explained: How to Identify Discontinuities and Their Significance

Introduction to Continuity at a Point

Definition of Continuity

Continuity is like the glue that holds the fabric of mathematics together. In simple terms, a function is continuous at a point if there are no breaks, jumps, or holes in its graph at that specific point. It means that the function flows smoothly without any abrupt changes.

Importance of Continuity in Mathematics

Continuity is a fundamental concept in mathematics, providing a solid foundation for many branches of the subject. It allows us to make precise statements about the behavior of functions and analyze their properties. Without continuity, our mathematical world would be full of random gaps and unpredictable behavior.

Understanding Discontinuities and Their Types

Definition of Discontinuity

Discontinuity, on the other hand, is the unruly cousin of continuity. It occurs when a function fails to be continuous at a particular point. In simple terms, there is a disturbance or disruption in the smooth flow of the function at that point.

Types of Discontinuities

Discontinuities come in various flavors. We have the removable discontinuity, where there is a hole in the function’s graph that can be “filled in” to make it continuous. Then, there’s the jump discontinuity, where the function makes a sudden leap from one value to another. Finally, we have the infinite discontinuity, where the function shoots off to infinity or negative infinity.

Examples and Characteristics of Each Discontinuity Type

Let’s take a closer look at these discontinuity types. For example, the function \(f(x) =\frac {x-1}{x-1}\) has a removable discontinuity at \(x = 1\). If we simplify the function by canceling out the common factor \((x-1)\), we can remove the hole and make it continuous.

Next, consider the function \(g(x) = floor(x)\), which gives the largest integer less than or equal to \(x\). This function has a jump discontinuity at every integer where it jumps from one value to the next without any intermediate values.

Lastly, imagine the function \(h(x) =\frac {1} {x}\). As \(x\) approaches \(zero\) from the right or left, the function tends towards infinity or negative infinity, respectively. This behavior indicates an infinite discontinuity.

Techniques for Identifying Discontinuities

Visual Inspection and Graphical Analysis

One way to identify discontinuities is to visually inspect the graph of a function. Look for breaks, holes, or jumps in the graph that disrupt the smooth flow. Pay attention to points where the function is undefined or exhibits unusual behavior.

Algebraic Methods and Mathematical Manipulation

Algebraic methods can also help identify discontinuities. Examine the function’s algebraic expression and look for values of \(x\) that cause division by \(zero\) or lead to undefined operations. Manipulate the expression to simplify it and uncover any removable discontinuities.

Utilizing Limits and Calculus

Limits and calculus provide powerful tools for detecting and analyzing discontinuities. By calculating limits from both the left and right sides of a point, we can determine if the function approaches different values or tends towards infinity. Calculus allows us to find derivatives and identify points where the function fails to be differentiable, a type of discontinuity.

The Significance of Discontinuities in Mathematics

Discontinuities as Critical Points

Discontinuities play a crucial role in mathematical analysis. They often mark significant points in a function, known as critical points, where interesting phenomena occur. Critical points can be points of interest for optimization, determining extrema, or studying the behavior of functions.

Implications for Function Behavior and Analysis

Studying discontinuities helps us understand the behavior of functions and their limitations. Discontinuities can indicate points of non-smoothness, abrupt changes, or singularities in a function. Analyzing them allows us to characterize the function’s behavior, identify regions of interest, and make informed decisions based on mathematical models.

In conclusion, understanding continuity and discontinuity is essential for navigating the mathematical landscape. Identifying and analyzing discontinuities provides valuable insights into the behavior of functions and allows us to make informed mathematical decisions. So, embrace the quirks and disruptions in your mathematical journey – they hold the key to unlocking a deeper understanding of the world of functions.

Common Examples of Discontinuities

Jump Discontinuity

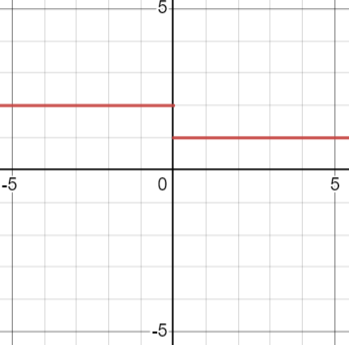
One of the most noticeable types of discontinuity is the jump discontinuity. Imagine a function that suddenly leaps from one value to another without any smooth transition in between. It’s like jumping off a cliff and landing on a completely different level. This kind of discontinuity can occur when there is a sudden change or a jump in the function’s values.

Example:

Removable Discontinuity

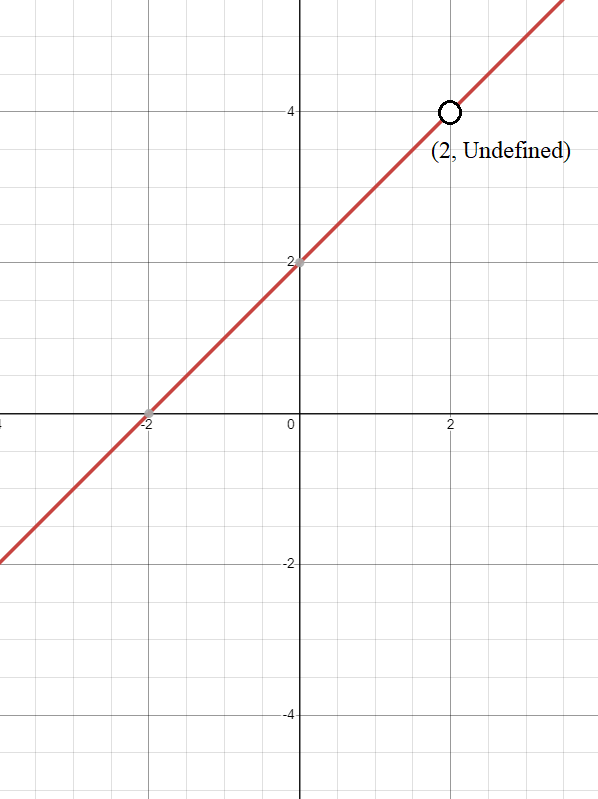
Unlike the jump discontinuity, the removable discontinuity can be “fixed” or removed by making a small adjustment to the function. It’s like having a hole in your favorite shirt that can be easily patched up. In this case, the function has a missing point or a hole at a specific point, but by redefining the function at that point, the discontinuity can be resolved.

Example:

\(f(x)=\frac{x^2-4}{x-2}\)

Infinite Discontinuity

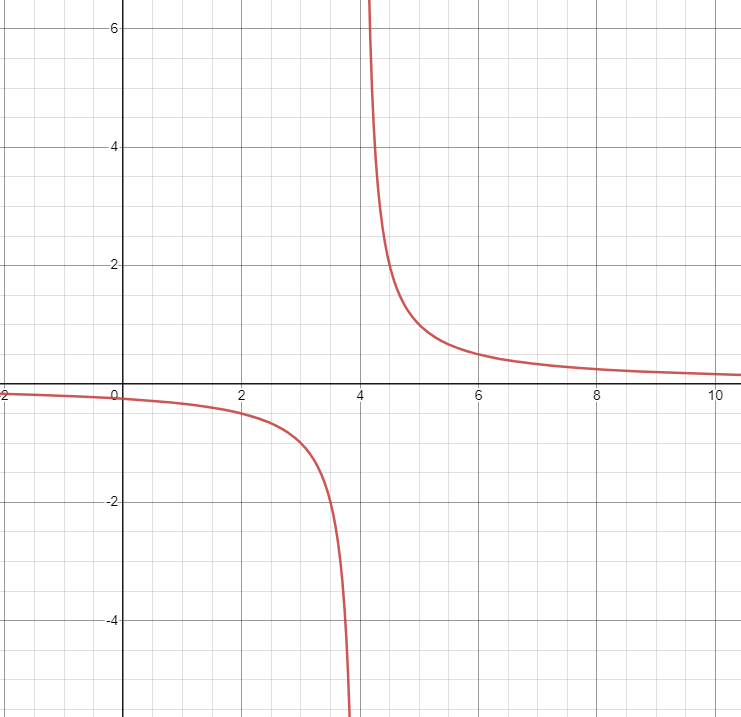
Imagine a function that goes haywire and starts shooting off towards infinity or negative infinity at a particular point. This is an infinite discontinuity. It’s like going from zero to a hundred in a split second. The function becomes unbounded, and its values shoot off towards infinity or negative infinity, which creates a discontinuity.

Example:

\(f(x=\frac1{x-4}\)

Analyzing the Effects of Discontinuities on Mathematical Functions

Discontinuities and Domain Restrictions

Discontinuities can have a significant impact on the domain of a function. A function may be defined and continuous everywhere except for certain points where it becomes discontinuous. These points then need to be excluded from the domain of the function to ensure its well-defined behavior.

Discontinuities and Limit Behavior

When a function encounters a discontinuity, its limit behavior can change dramatically. Approaching a point of discontinuity from different directions can yield different results. The function might not have a well-defined limit at the point of discontinuity, making it challenging to analyze its behavior in that vicinity.

Discontinuities and Graphical Representation

Graphically, discontinuities show up as breaks, jumps, or holes in the function’s plot. These visual representations help us visualize the behavior of the function and understand where the discontinuities occur. By examining the graph, we can identify the type of discontinuity and how it affects the function’s behavior.

Strategies for Addressing Discontinuities in Calculus and Analysis

Continuity and Its Relationship to Differentiability

Continuity and differentiability go hand in hand. If a function is differentiable at a point, it must also be continuous at that point. Understanding the relationship between continuity and differentiability is crucial in analyzing and resolving discontinuities in calculus and analysis.

Techniques for Removing or Mitigating Discontinuities

For removable discontinuities, various techniques can be employed to “fix” the function and remove the discontinuity. These techniques involve redefining the function or filling the missing point, allowing for a smooth transition of values.

Introducing Piecewise Functions

Piecewise functions are a powerful tool for addressing more complex discontinuities. Instead of trying to resolve a discontinuity within a single function, piecewise functions allow us to define different expressions for specific intervals, effectively adapting to the discontinuous behavior in a more systematic manner.

Real-World Applications of Continuity and Discontinuity

Engineering and Design

In engineering and design, continuity and discontinuity play vital roles. Understanding the behavior of functions and their discontinuities helps engineers design stable structures, efficient systems, and smooth operations.

Economics and Financial Modeling

Economics and financial modeling heavily rely on mathematical functions and their continuity properties. Discontinuities can represent critical points such as market crashes, sudden policy changes, or shifts in supply and demand, influencing decision-making and risk analysis.

Physics and Natural Sciences

Physics and natural sciences utilize mathematical models to understand the behavior of physical phenomena. Continuity and discontinuity concepts are crucial in accurately representing and predicting physical processes, such as phase transitions, particle interactions, and wave propagation.

Understanding continuity at a point and identifying discontinuities is crucial for various mathematical disciplines. By being able to recognize and analyze these disruptions, mathematicians can accurately interpret the behavior of functions and make informed calculations. Whether it be in calculus, analysis, or real-world applications, the significance of continuity and discontinuity cannot be understated. By delving into the types of discontinuities, their identification techniques, and their impact on function behavior, we have equipped ourselves with the tools necessary to navigate the intricacies of mathematical continuity. Armed with this knowledge, we can confidently approach mathematical problems and appreciate the beauty and complexity of this fundamental concept.

FAQ

1. What is the difference between continuity and discontinuity in mathematics?

Continuity refers to the smooth and uninterrupted behavior of a mathematical function at a specific point, whereas discontinuity represents a disruption in this smoothness, resulting in abrupt changes or gaps in the function’s behavior.

2. How do discontinuities affect mathematical functions?

Discontinuities can have significant effects on the behavior and analysis of mathematical functions. They can render functions non-differentiable, pose challenges in evaluating limits, and alter the graphical representation of the function, often leading to unexpected or ambiguous results.

3. Are there different types of discontinuities?

Yes, there are several types of discontinuities. Some common types include jump discontinuities, where the function makes a sudden jump between two distinct values; removable discontinuities, where the function has a hole or gap that can be filled to make it continuous; and infinite discontinuities, where the function approaches positive or negative infinity at a specific point.

4. How can I identify and analyze discontinuities in mathematical functions?

Discontinuities can be identified through visual inspection of the graph, looking for abrupt changes, gaps, or vertical asymptotes. Algebraic methods, such as factoring and simplification, can also help in identifying removable discontinuities. Calculus techniques, including limits and derivatives, can be employed to analyze the behavior and nature of discontinuities in more complex functions.