Infinitely Close But Never There

An asymptote is a line that a graph of a function approaches but never actually reaches. Understanding asymptotes is crucial in calculus and analysis as they provide insight into the behavior of functions as they move towards infinity or near critical points. There are three primary types of asymptotes: vertical, horizontal, and oblique.

1. Vertical Asymptotes

Vertical asymptotes occur when the function approaches infinity or negative infinity as the input approaches a certain value. They are typically found in rational functions where the denominator can be zero. The formula for finding a vertical asymptote is derived by setting the denominator equal to zero and solving for the variable.

For instance, consider the function \( f(x) = \frac{1}{x-2} \). The vertical asymptote is found by setting the denominator \( x-2 = 0 \), which gives \( x = 2 \). This means there’s a vertical asymptote at \( x = 2 \).

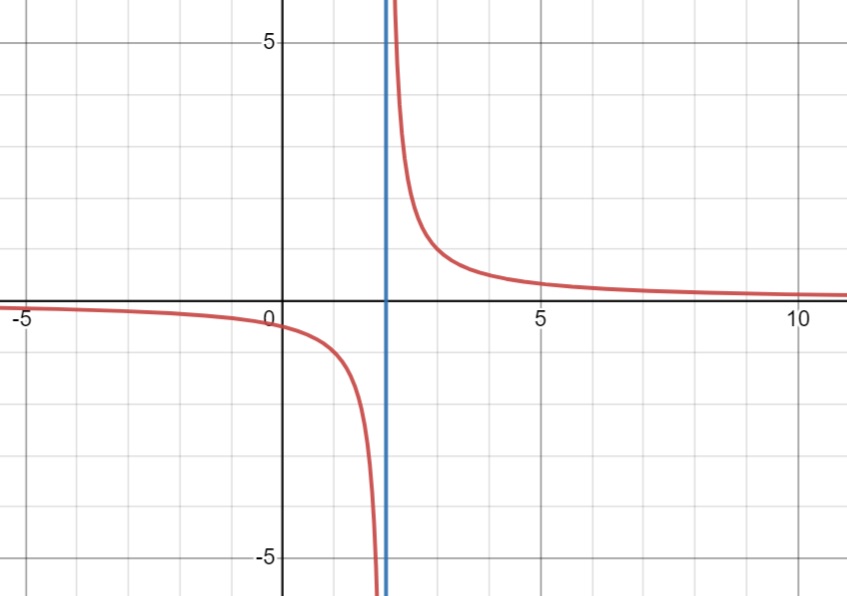
2. Horizontal Asymptotes

Horizontal asymptotes describe the behavior of a graph as the input goes to positive or negative infinity. They occur in functions where the degree of the numerator and the denominator determines the asymptote. In rational functions, if the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is the x-axis \( y=0 \). If the degrees are equal, the horizontal asymptote is the ratio of the leading coefficients.

Consider the rational function \( f(x) = \frac{5x^3 + 2x + 1}{x^3 + 3} \). In this case, we examine the behavior of the function as \( x \) approaches infinity or negative infinity.

For horizontal asymptotes in rational functions, we look at the leading terms in both the numerator and the denominator. Here, the leading term in both the numerator and the denominator is \( x^3 \). As \( x \) approaches infinity, the lower-degree terms become insignificant compared to the leading terms. Therefore, the behavior of the function is dominated by the ratio of the coefficients of the leading terms.

The horizontal asymptote is thus determined by the ratio of the coefficients of \( x^3 \) in the numerator and the denominator. In this case, it is \( \frac{5}{1} \), or simply \( 5 \). Therefore, the horizontal asymptote of the function ( f(x) ) is the line \( y = 5 \). This means as \( x \) goes to infinity or negative infinity, the function approaches the line \( y = 5 \) but never actually reaches it.

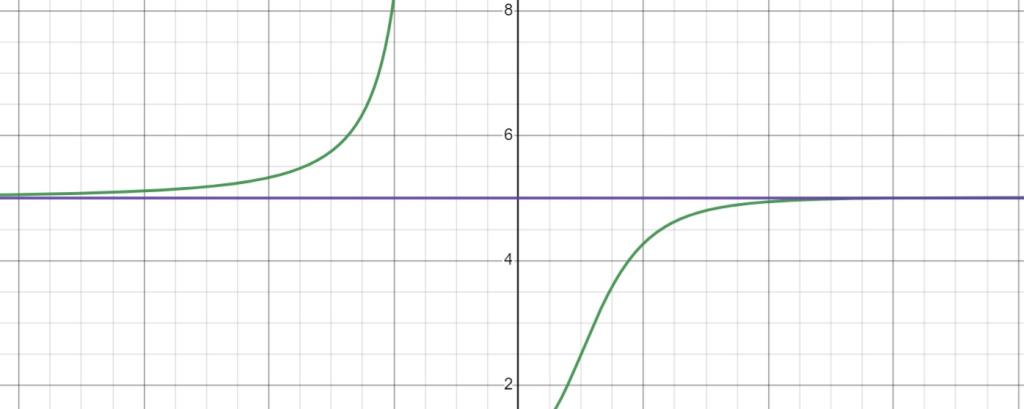
3. Oblique (Slant) Asymptotes

Oblique or slant asymptotes occur when the degree of the numerator is exactly one more than the degree of the denominator in a rational function. To find an oblique asymptote, divide the numerator by the denominator. The quotient (excluding the remainder) is the equation of the oblique asymptote.

Consider \( h(x) = \frac{2x^2 + 3x + 1}{x + 2} \). Dividing \( 2x^2 + 3x + 1 \) by \( x + 2 \) gives a linear polynomial \( 2x -1 \) as the oblique asymptote.

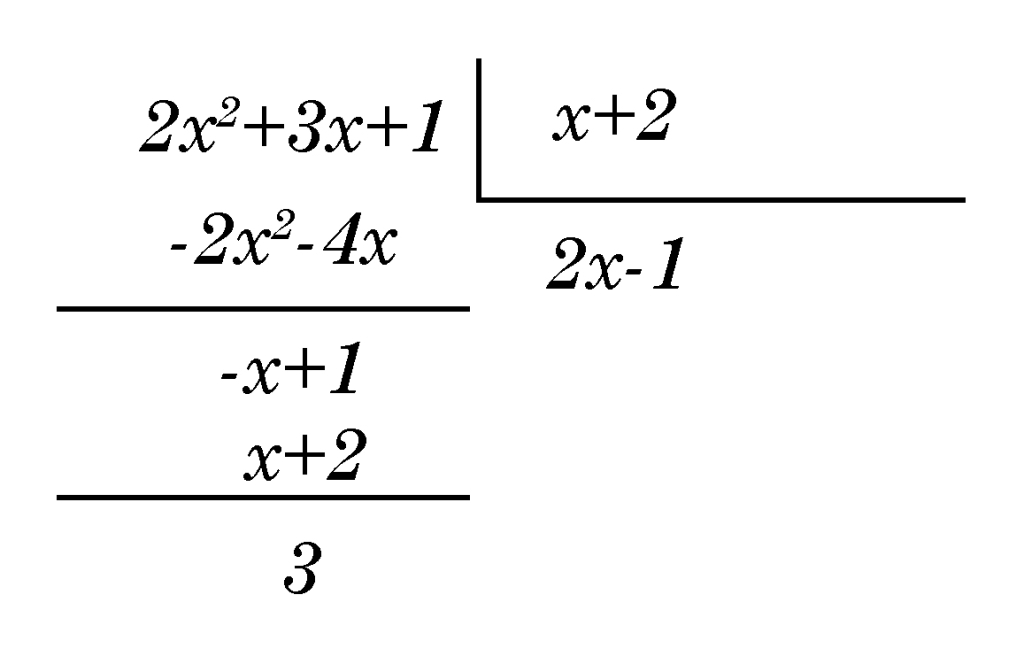
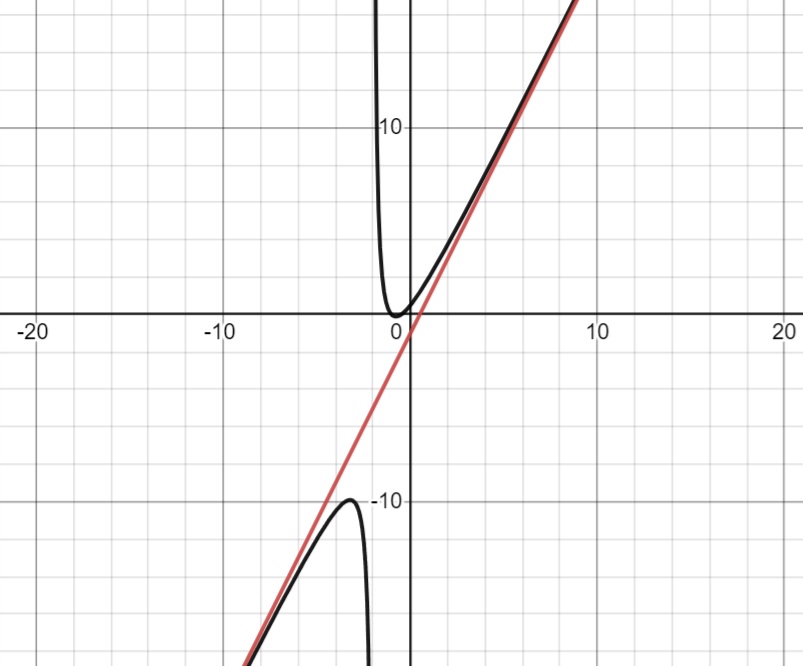
Asymptotes are not just theoretical concepts; they have practical applications in physics, engineering, and economics, especially in modeling scenarios where certain limits are approached but not reached. Understanding the behavior of asymptotes allows for a deeper comprehension of the limits and behavior of functions, which is essential in many fields of science and mathematics.