How to Graph Solutions to Linear Inequalities?

A Step-by-step Guide to Graph Solutions to Linear Inequalities

The steps to graphing solutions to linear inequalities on a number line are:

Step 1: Identifying the inequality you want to graph

Start by identifying the inequality you want to graph. An inequality is a statement that compares two expressions using symbols like \(“<“\) (less than), \(“>”\) (greater than), \(“≤”\) (less than or equal to), \(“≥”\) (greater than or equal to).

Step 2: Rewrite the inequality

Rewrite the inequality with the variable on the left and the constant on the right if it is not already in that form.

Step 3: Draw a number line and label it

Draw a number line and label it with the values that are relevant to the inequality. For example, if the inequality involves the variable \(“x”\), label the number line with the values of \(“x”\) that are relevant to the inequality. If the inequality involves a constant, label the number line with the values of the constant that are relevant to the inequality.

Step 4: Draw a circle on the number line

Draw an open or closed circle on the number line at the point that corresponds to the constant in the inequality.

Step 5: Draw an arrow pointing in the direction

Draw an arrow pointing in the direction that includes the solutions to the inequality. If the inequality is \(“<“\) or \(“>”\), the arrow should point in the direction of the numbers that satisfy the inequality. If the inequality is \(“≤”\) or \(“≥”\), the arrow should point in both directions since the endpoints of the range of solutions are included in the solutions.

Step 6: Label the shaded region to indicate which inequality it represents

You can use an arrow pointing in the direction of the shaded region to indicate that it represents all the numbers that satisfy the inequality.

Step 7: Repeat these steps for any additional inequalities that you need to graph

The solution to a system of linear inequalities is the intersection of the ranges of numbers represented by the shaded regions on the number line.

By following these steps, you can graph solutions to linear inequalities on a number line.

Graphing Solutions to Linear Inequalities – Examples 1

Graph the solution to the inequality \(2x + 3 < 9\).

Solution:

To graph this inequality on a number line, we need to isolate the variable \(x\) on one side of the inequality. Subtracting \(3\) from both sides, we get:

\(2x < 6\)

Now, dividing both sides by \(2\), we get:

\(x < 3\)

To graph this solution on a number line, we start by drawing a line and marking a point at \(3\). Since \(x\) is less than \(3\), we shade the region to the left of the point. The graph should look like this:

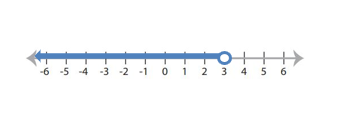
Graphing Solutions to Linear Inequalities – Examples 2

Graph the solution to the inequality \(-4x + 2 ≥ -6x – 1\).

Solution:

To graph this inequality on a number line, we need to isolate the variable \(x\) on one side of the inequality. Adding \(6x\) to both sides, we get:

\(2x + 2 ≥ -1\)

Now, subtracting \(2\) from both sides, we get:

\(2x ≥ -3\)

Finally, dividing both sides by \(2\), we get:

\(x ≥ -\frac{3}{2}\)

To graph this solution on a number line, we start by drawing a line and marking a point at \(-\frac{3}{2}\). Since \(x\) is greater than or equal to \(-\frac{3}{2}\), we shade the region to the right of the point. The graph should look like this:

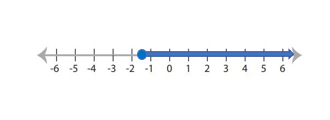
Exercises for Graphing Solutions to Linear Inequalities

Graph the solution of each inequality.

1. \(\color{blue}{4x+3\ge 2x+11}\)
2. \(\color{blue}{\frac{x}{9}-6\le 4}\)

• \(\color{blue}{4x+3\ge 2x+11}\)

• \(\color{blue}{\frac{x}{9}-6\le 4}\)