How to Solve Systems of Linear Inequalities?

The solution to a system of a linear inequality is the region where the graphs of all linear inequalities in the system overlap.

Related Topics

• How to Solve Linear Inequalities
• How to Solve Quadratic Inequalities

A step-by-step guide to solving systems of linear inequalities

The system of linear inequalities is a set of equations of linear inequality containing the same variables. Several methods of solving systems of linear equations translate to the system of linear inequalities. However, solving a system of linear inequalities is somewhat different from linear equations because the signs of inequality prevent us from solving by the substitution or elimination method. Perhaps the best way to solve systems of linear inequalities is by graphing the inequalities.

To solve a system of inequalities, graph each linear inequality in the system on the same \(x-y\) axis by following the steps below:

1. Solve the inequality for \(y\).
2. Treat the inequality as a linear equation and graph the line as either a solid line or a dashed line depending on the inequality sign. If the inequality sign does not contain an equals sign \((< or >)\) then draw the line as a dashed line. If the inequality sign does have an equals sign \((≤ or ≥)\) then draw the line as a solid line.
3. Shade the region that satisfies the inequality.
4. Repeat steps \(1 – 3\) for each inequality.
5. The solution set will be the overlapped region of all the inequalities.

Solving Systems of Linear Inequalities – Example 1:

Solve the following system of inequalities.

\(\begin{cases}x\:-\:5y\ge \:6\\ \:3x\:+\:2y>1\end{cases}\)

Solution:

First, isolate the variable \(y\) to the left in each inequality:

\(x -5y≥ 6\)

\(x≥6 + 5y\)

\(5y≤ x- 6\)

\(y≤0.2 x -1.2\)

And:

\(3x+ 2y> 1\)

\(2y>1-3x\)

\(y> 0.5-1.5x\)

Now, graph \(y≤ 0.2x-1.2\) and \(y > 0.5 -1.5x\) using a solid line and a broken one, respectively.

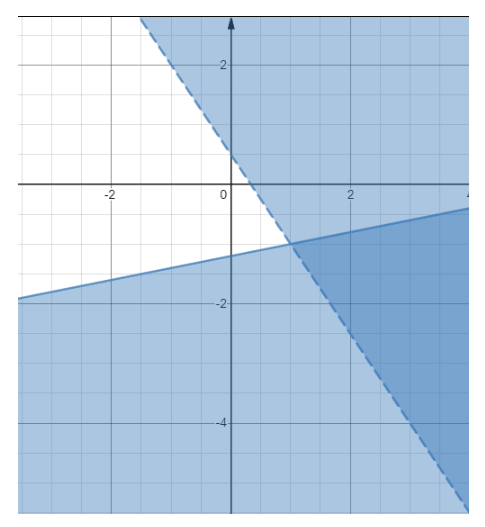
The solution of the system of inequality is the darker shaded area which is the overlap of the two individual solution regions.

Exercises for Solving Systems of Linear Inequalities

Determine the solution to the following system of inequalities.

• \(\color{blue}{\begin{cases}5x-2y\le 10 \\ \:3x+2y>\:6\end{cases}}\)

• \(\color{blue}{\begin{cases}-2x-y<\:-1 \\ \:4x+\:2y\:\le -6\end{cases}}\)

• \(\color{blue}{\begin{cases}5x-2y\le 10 \\ \:3x+2y>\:6\end{cases}}\)

• \(\color{blue}{\begin{cases}-2x-y<\:-1 \\ \:4x+\:2y\:\le -6\end{cases}}\)