How to Use Models to Compare Fractions?
Comparing fractions involves finding out what fraction is bigger or lesser. In this step-by-step guide, you will learn to use models to compare fractions.
A Step-by-step guide to using models to compare fractions
You can utilize these models for comparing fractions!
Comparing fractions involves finding out what fraction is bigger or lesser.
For comparing fractions having area models, the size of the whole has to be the same!
Fraction bar models are whenever one draws a long rectangle and then divides it into identical portions to reveal the fraction. A denominator is the number of equal parts that the bar gets divided into. A numerator informs one of the number of parts that should be colored. Then, you must look at the colored areas to decide what fraction is smaller, larger, or equivalent.
The Absolute Best Book for 4th Grade Students
Using Models to Compare Fractions-Example 1:
Which model represents the greater fraction?
a)
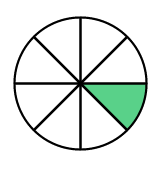
b)
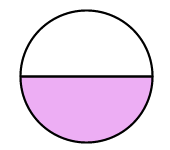
Solution: Both figures have \(1\) colored parts but the second figure is bigger. This is because shape \(a\) is divided into \(8\) parts but shape \(b\) is sliced into \(2\) parts.
\(\frac{1}{2}>\frac{1}{8}\)
A Perfect Book for Grade 4 Math Word Problems!
Exercises for Using Models to Compare Fractions
Which model represents the greater fraction?
a)
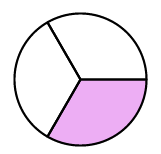
b)
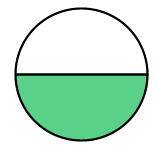
c)
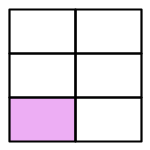
d)
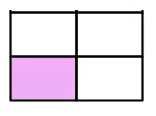
- \(\color{blue}{B}\)
- \(\color{blue}{D}\)
The Best Math Books for Elementary Students
Related to This Article
More math articles
- How is the ASVAB Test Scored?
- Repeating Decimals
- SAT Math Vs. High School Math
- Top 10 4th Grade ACT Aspire Math Practice Questions
- How to Find Slope? (+FREE Worksheet!)
- Properties of the Horizontal Line
- How to Deciphering the Puzzle of Time: A Step-by-Step Guide to Solving Age Problems in Mathematics
- 3rd Grade WY-TOPP Math Worksheets: FREE & Printable
- How to Unlock the Secrets: “SIFT Math for Beginners” Solution Manual
- How to Multiply and Divide Complex Numbers in Polar Form?
What people say about "How to Use Models to Compare Fractions? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.