How to Graph Linear Inequalities? (+FREE Worksheet!)
Learn how to graph linear inequalities using a testing point in a few simple steps.
[include_netrun_products_block from-products="product/the-most-comprehensive-ftce-math-preparation-bundle-includes-ftce-math-prep-books-workbooks-and-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{{url}}/?ajax-add-to-cart={{id}}" product-item-button-custom-url-if-not-salable="{{productUrl}} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Watch this practice video for additional examples and reinforcement:
Related Topics
- How to Find Midpoint
- How to Find Distance of Two Points
- How to Find Slope
- How to Write Linear Equations
- How to Graph Lines by Using Standard Form
Step by step guide to graphing linear inequalities
- First, graph the “equals” line.
- Choose a testing point. (it can be any point on both sides of the line.)
- Put the value of \((x, y)\) of that point in the inequality. If that works, that part of the line is the solution. If the values don’t work, then the other part of the line is the solution.
For education statistics and research National Center for Education Statistics.
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Graphing Linear Inequalities – Example 1:
Sketch the graph of \(y<2x-4\).
Solution:
First, graph the line:
\(y=2x-4\). The slope is \(2\) and \(y\)-intercept is \(-4\).
Then, choose a testing point. The easiest point to test is the origin: \((0,0)\)
\((0,0)→y<2x-4→0<2(0)-4→0<-4\)
\(0\) is not less than \(-4\). So, the other part of the line (on the right side) is the solution.
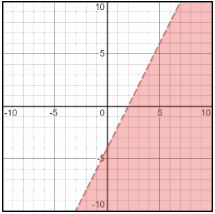
Graphing Linear Inequalities – Example 2:
Sketch the graph of \(y<2x-3\).
Solution:
First, graph the line:
\(y=2x-3\). The slope is \(2\) and \(y\)-intercept is \(-3\).
Then, choose a testing point. The easiest point to test is the origin: \((0,0)\)
\((0,0)→y<2x-3→0<2(0)-3→0<-3\)
\(0\) is not less than \(-3\). So, the other part of the line (on the right side) is the solution.
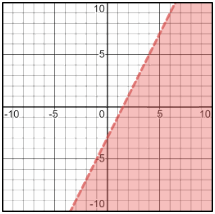
Exercises for Graphing Linear Inequalities
Sketch the graph of each linear inequality.
- \(\color{blue}{y < – 4x + 2}\)
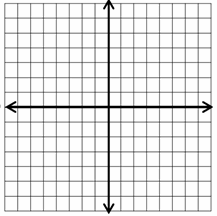
- \(\color{blue}{2x + y < – 4}\)
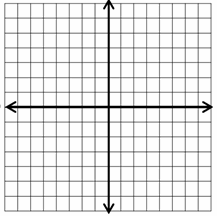
Download Graphing Linear Inequalities Worksheet
- \(\color{blue}{y < – 4x + 2}\)
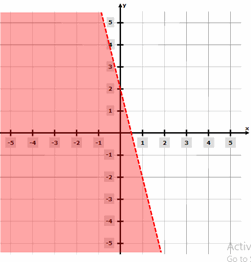
- \(\color{blue}{2x + y < – 4}\)
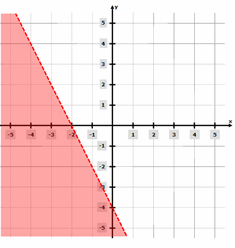
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- How to Solve One-Step Inequalities? (+FREE Worksheet!)
- Overview of the HiSET Mathematics Test
- FREE SSAT Lower Level Math Practice Test
- CHSPE Math-Test Day Tips
- How to Motivate Anyone to Start Learning Algebra and Geometry
- How to Identify Graphs of Basic Functions
- Top Tablets for Online Math Teaching
- Everything You Need to Know about Indeterminate and Undefined Limits
- How to Convert Repeating Decimals to Fractions? (+FREE Worksheet!)
- A Comprehensive Collection of Free PERT Math Practice Tests
What people say about "How to Graph Linear Inequalities? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.