How to Graph Lines by Using Standard Form? (+FREE Worksheet!)
Learn how to graph lines by using the equation of the line in standard form.
Related Topics
- How to Find Midpoint
- How to Find Distance of Two Points
- How to Find Slope
- How to Graph Linear Inequalities
- How to Write Linear Equations
Step by step guide to graphing lines using the standard form
- Find the \(x\)-intercept of the line by putting zero for \(y\).
- Find the \(y\)- intercept of the line by putting zero for the \(x\).
- Connect these two points.
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Graphing Lines Using Standard Form – Example 1:
Sketch the graph of \(x-y=\ – 2\)
Solution:
First isolate \(y\) for \(x: x-y=-2→y=x+2\)
Find the \(x\)−intercept of the line by putting zero for \(y\).
\(y=x+2→x+2=0→x=-2 \)
Find the \(y\)−intercept of the line by putting zero for the \(x\).
\(y=x+2 → y=0+2→y=2 \)
Then: \(x\)−intercept: \((-2,0)\) and \(y\)−intercept: \((0,2)\)
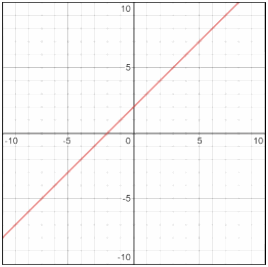
Graphing Lines Using Standard Form – Example 2:
Sketch the graph of \(x-y= -5\).
Solution:
First isolate \(y\) for \(x: x-y=-5→y=x+5\)
Find the \(x−\)intercept of the line by putting zero for \(y\).
\( y=x+5→x+5=0→x=-5 \)
Find the \(y−\)intercept of the line by putting zero for the \(x\).
\(y=x+5 → y=0+5→y=5\)
Then: \(x−\)intercept: \((-5,0)\) and \(y−\)intercept: \((0,5)\)
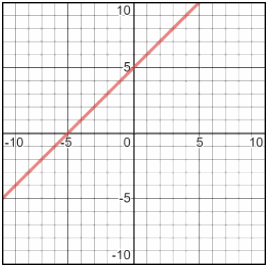
Exercises for Graphing Lines Using Standard Form
Sketch the graph of each line.
- \(\color{blue}{2x – y = 4}\)
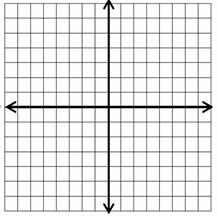
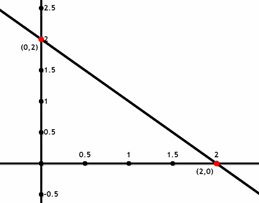
- \(\color{blue}{x + y = 2}\)
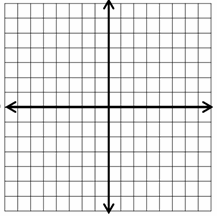
- \(\color{blue}{2x – y = 4}\)
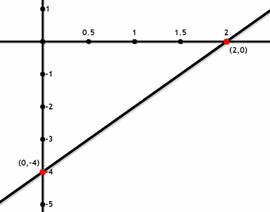
- \(\color{blue}{x + y = 2}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- Top 10 Tips to Create an AFOQT Math Study Plan
- 10 Most Common 3rd Grade OST Math Questions
- A Comprehensive Guide to the Properties of Rhombuses
- Debating Tailoring Your Study Plans To Suit Your Learning Styles? Here’s Why You Should
- Top Proven Strategies To Increase Your SAT Math Score
- The Ultimate PSAT 10 Math Formula Cheat Sheet
- How to Prepare for the FSA Math Test?
- 10 Most Common 3rd Grade NYSE Math Questions
- How to Solve Arithmetic Sequences? (+FREE Worksheet!)
- The Ultimate 7th Grade K-PREP Math Course (+FREE Worksheets)
What people say about "How to Graph Lines by Using Standard Form? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.