How to Graph an Equation in the Standard Form?

A step-by-step Guide to Graph an Equation in the Standard Form

Here are the steps to graph an equation in standard form:

Step 1: Find the \(x\) and \(y\)-intercepts

The \(x\)-intercept is the point where the equation intersects the \(x\)-axis, and the \(y\)-intercept is the point where the equation intersects the \(y\)-axis. To find the \(x\)-intercept, set \(y = 0\) in the equation and solve for \(x\). To find the \(y\)-intercept, set \(x = 0\) in the equation and solve for \(y\).

Step 2: Plot the intercepts

Mark the \(x\)-intercept on the \(x\)-axis and the \(y\)-intercept on the \(y\)-axis. These two points will help you sketch the line.

Step 3: Determine the slope

The slope of the line is the ratio of the change in \(y\) to the change in \(x\). Rearrange the equation in slope-intercept form \((y = mx + b)\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. To find the slope, divide the coefficient of \(x\) by the coefficient of \(y\), and simplify if possible.

Step 4: Plot additional points

To sketch the line, you need at least one additional point. Choose any value of \(x\), plug it into the equation, and solve for \(y\). This will give you the coordinates of another point on the line. Plot this point on the coordinate plane.

Step 5: Sketch the line

Use a straight edge or ruler to draw a line through the intercepts and the additional point. This line represents the graph of the equation.

Graph an Equation in the Standard Form – Examples 1

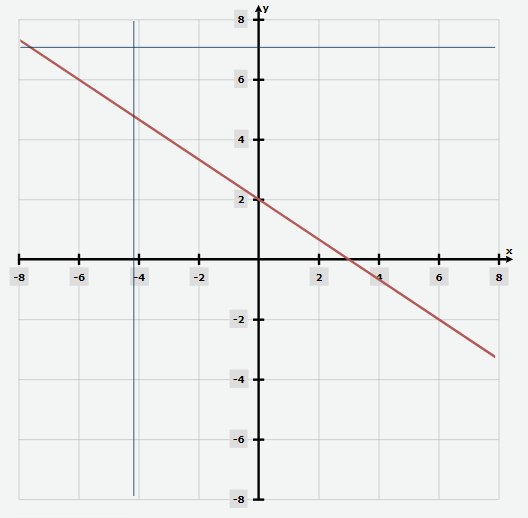
Graph the equation \(2x + 3y = 6\)

Solution:

Step 1: Find the intercepts.
To find the \(x\)-intercept, set \(y = 0: 2x + 3(0) = 6\), so \(x = 3\). The \(x\)-intercept is \((3,0)\).
To find the \(y\)-intercept, set \(x = 0: 2(0) + 3y = 6\), so \(y = 2\). The \(y\)-intercept is (0,2).

Step 2: Plot the intercepts.
Mark the \(x\)-intercept \((3,0)\) on the \(x\)-axis and the \(y\)-intercept \((0,2)\) on the \(y\)-axis.

Step 3: Determine the slope.
Rearrange the equation in slope-intercept form: \(3y = -2x + 6\), so \(y = (-\frac{2}{3})x + 2\). The slope is \(-\frac{2}{3}\).

Step 4: Plot additional points.
Choose any value of \(x\), such as \(x =9\), and solve for \(y: 2(9) + 3y = 6\), so \(y = 0\). Point \((9,-4)\) is on the line.

Step 5: Sketch the line.
Use a straight edge or ruler to draw a line through the intercepts and the additional point. The line represents the graph of the equation.

The graph of the equation \(2x + 3y = 6\) is a straight line passing through the points \((3,0)\) and \((0,2)\).

Exercises for Graph an Equation in the Standard Form

Graph each equation.

• \(\color{blue}{4x+2y=8}\)

• \(\color{blue}{3x+5y=15}\)

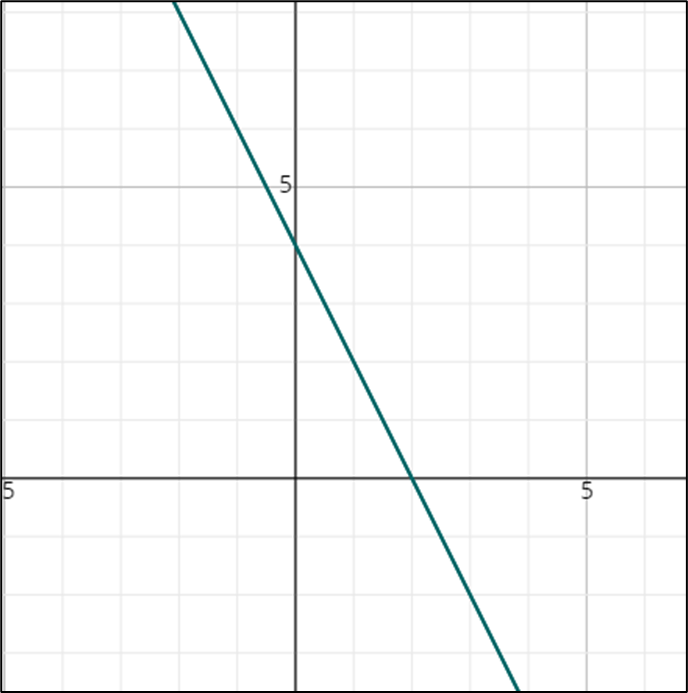
• \(\color{blue}{4x+2y=8}\)

• \(\color{blue}{3x+5y=15}\)