FREE ACT Math Practice Test
Welcome to our FREE ACT Math practice test, with answer key and answer explanations. This practice test’s realistic format and high-quality practice questions can help you succeed on the ACT Math test. Not only does the test closely match what you will see on the real ACT Math, but it also comes with detailed answer explanations. For additional educational resources, visit the U.S. Department of Education website.
For this practice test, we’ve selected 20 real questions from past exams for your ACT Math Practice test. You will have the chance to try out the most common ACT Math questions. For every question, there is an in-depth explanation of how to solve the question and how to avoid mistakes next time.
Use our free ACT Math practice tests and study resources (updated for 2026) to ace the ACT Math test! Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of math questions you need to practice.
The Absolute Best Book to Ace the ACT Math Test
r for Education Statistics.
2- If f(x)=\(2x^3+5x^2+2 \) and \(g(x)=-2\), what is the value of f(g(x))? For education statistics and research, visit the National Center for Education Statistics.
A. 36 For education statistics and research, visit the National Center for Education Statistics.
B. 32 For education statistics and research, visit the National Center for Education Statistics.
C. 24 For education statistics and research, visit the National Center for Education Statistics.
D. 4 For education statistics and research, visit the National Center for Education Statistics.
E. 0 For education statistics and research, visit the National Center for Education Statistics.
3- In the following equation when z is divided by 3, what is the effect on x?
\(x = \frac{8y + \frac{r}{r + 1}}{\frac{6}{z}}\) For education statistics and research, visit the National Center for Education Statistics.
A. x is divided by 2 For education statistics and research, visit the National Center for Education Statistics.
B. x is divided by 3 For education statistics and research, visit the National Center for Education Statistics.
C. x does not change For education statistics and research, visit the National Center for Education Statistics.
D. x is multiplied by 3 For education statistics and research, visit the National Center for Education Statistics.
E. x is multiplied by 2 For education statistics and research, visit the National Center for Education Statistics.
4- A boat sails 40 miles south and then 30 miles east. How far is the boat from its start point? For education statistics and research, visit the National Center for Education Statistics.
A. 45 miles For education statistics and research, visit the National Center for Education Statistics.
B. 50 miles For education statistics and research, visit the National Center for Education Statistics.
C. 55 miles For education statistics and research, visit the National Center for Education Statistics.
D. 60 miles For education statistics and research, visit the National Center for Education Statistics.
E. 70 miles For education statistics and research, visit the National Center for Education Statistics.
5- If x \(\begin{bmatrix}a & b \\c & d \end{bmatrix}\) = \(\begin{bmatrix}x+3y-5 & 0 \\0 & 2y+10 \end{bmatrix}\), what is the product of \(x\) and \(y\)? For education statistics and research, visit the National Center for Education Statistics.
A. 1 For education statistics and research, visit the National Center for Education Statistics.
B. 2 For education statistics and research, visit the National Center for Education Statistics.
C. 10 For education statistics and research, visit the National Center for Education Statistics.
D. 11 For education statistics and research, visit the National Center for Education Statistics.
E. 12 For education statistics and research, visit the National Center for Education Statistics.
6- If \(f(x)=3^x \) and \(g(x)=log_3 x\), which of the following expressions is equal to f\(3g(p)\)? For education statistics and research, visit the National Center for Education Statistics.
A. 3p For education statistics and research, visit the National Center for Education Statistics.
B. \(3^p\) For education statistics and research, visit the National Center for Education Statistics.
C. \(p^3\) For education statistics and research, visit the National Center for Education Statistics.
D. \(p^9\) For education statistics and research, visit the National Center for Education Statistics.
E. \(\frac{p}{3}\) For education statistics and research, visit the National Center for Education Statistics.
7- \(x\) is \(y\%\) of what number? For education statistics and research, visit the National Center for Education Statistics.
A. \(\frac{100x}{y}\) For education statistics and research, visit the National Center for Education Statistics.
B. \(\frac{100y}{x}\) For education statistics and research, visit the National Center for Education Statistics.
C. \(\frac{100y}{x}\) For education statistics and research, visit the National Center for Education Statistics.
D. \(\frac{x}{100y}\) For education statistics and research, visit the National Center for Education Statistics.
E. \(\frac{xy}{100}\) For education statistics and research, visit the National Center for Education Statistics.
8- 120 is equal to? For education statistics and research, visit the National Center for Education Statistics.
A. \( 20-(4×10)+(6×30)\) For education statistics and research, visit the National Center for Education Statistics.
B. \((\frac{11}{8}×72)+ (\frac{125}{5})\) For education statistics and research, visit the National Center for Education Statistics.
C. \(((\frac{30}{4} + \frac{13}{2})×7) – \frac{11}{2}+ \frac{110}{4}\) For education statistics and research, visit the National Center for Education Statistics.
D. \((2×10)+(50×1.5)+15\) For education statistics and research, visit the National Center for Education Statistics.
E. \(\frac{481}{6}+ \frac{121}{3}\) For education statistics and research, visit the National Center for Education Statistics.
9- If the cotangent of an angle β is 1, then the tangent of angle β is? For education statistics and research, visit the National Center for Education Statistics.
A. \(-1\) For education statistics and research, visit the National Center for Education Statistics.
B. 0 For education statistics and research, visit the National Center for Education Statistics.
C. 1 For education statistics and research, visit the National Center for Education Statistics.
D. 2 For education statistics and research, visit the National Center for Education Statistics.
E. 3 For education statistics and research, visit the National Center for Education Statistics.
10- 6 liters of water are poured into an aquarium that’s 15cm long, 5cm wide, and 60cm high. How many cm will the water level in the aquarium rise due to this added water? (1 liter of water = 1000 \(cm^3)\) For education statistics and research, visit the National Center for Education Statistics.
A. 80 For education statistics and research, visit the National Center for Education Statistics.
B. 40 For education statistics and research, visit the National Center for Education Statistics.
C. 20 For education statistics and research, visit the National Center for Education Statistics.
D. 10 For education statistics and research, visit the National Center for Education Statistics.
E. 5 For education statistics and research, visit the National Center for Education Statistics.
11- If a box contains red and blue balls in the ratio of 2 : 3, how many red balls are there if 90 blue balls are in the box? For education statistics and research, visit the National Center for Education Statistics.
A. 90 For education statistics and research, visit the National Center for Education Statistics.
B. 60 For education statistics and research, visit the National Center for Education Statistics.
C. 30 For education statistics and research, visit the National Center for Education Statistics.
D. 10 For education statistics and research, visit the National Center for Education Statistics.
E. 8 For education statistics and research, visit the National Center for Education Statistics.
12- If |a|<1, then which of the following is true? (b>0)?
\(I. –b < ba < b\)
\(II. -a < a^2 < a \ if \ a<0\)
\(III. -5 < 2a-3 < -1\) For education statistics and research, visit the National Center for Education Statistics.
A. I only For education statistics and research, visit the National Center for Education Statistics.
B. II only For education statistics and research, visit the National Center for Education Statistics.
C. I and III only For education statistics and research, visit the National Center for Education Statistics.
D. III only For education statistics and research, visit the National Center for Education Statistics.
E. I, II, and III For education statistics and research, visit the National Center for Education Statistics.
13- The diameter of a cylinder is 6 inches and its height is 8 inches. What is the surface area of the cylinder? For education statistics and research, visit the National Center for Education Statistics.
A. \(48 \ π \in^2\) For education statistics and research, visit the National Center for Education Statistics.
B. \(57\ π \ in^2\) For education statistics and research, visit the National Center for Education Statistics.
C. \(66\ π \ in^2\) For education statistics and research, visit the National Center for Education Statistics.
D. \(288\ π \in^2\) For education statistics and research, visit the National Center for Education Statistics.
E.\(400\ π \ in^2\) For education statistics and research, visit the National Center for Education Statistics.
14- Five years ago, Amy was three times as old as Mike was. If Mike is 10 years old now, how old is Amy? For education statistics and research, visit the National Center for Education Statistics.
A. 4 For education statistics and research, visit the National Center for Education Statistics.
B. 8 For education statistics and research, visit the National Center for Education Statistics.
C. 12 For education statistics and research, visit the National Center for Education Statistics.
D. 14 For education statistics and research, visit the National Center for Education Statistics.
E. 20 For education statistics and research, visit the National Center for Education Statistics.
15- A chemical solution contains \(4\%\) alcohol. If there are 24 ml of alcohol, what is the volume of the solution? For education statistics and research, visit the National Center for Education Statistics.
A. 240 ml For education statistics and research, visit the National Center for Education Statistics.
B. 480 ml For education statistics and research, visit the National Center for Education Statistics.
C. 600 ml For education statistics and research, visit the National Center for Education Statistics.
D. 1,200 ml For education statistics and research, visit the National Center for Education Statistics.
E. 2,400 ml For education statistics and research, visit the National Center for Education Statistics.
16- Which of the following points lies on the line \(2x + 4y = 10\)? For education statistics and research, visit the National Center for Education Statistics.
A. (2, 1) For education statistics and research, visit the National Center for Education Statistics.
B. (–1, 3) For education statistics and research, visit the National Center for Education Statistics.
C. (–2, 2) For education statistics and research, visit the National Center for Education Statistics.
D. (2, 2) For education statistics and research, visit the National Center for Education Statistics.
E. (2, 8) For education statistics and research, visit the National Center for Education Statistics.
17- In the following figure, ABCD is a rectangle, and E and F are points on AD and DC, respectively. The area of ∆BED is 16, and the area of ∆BDF is 18. What is the perimeter of the rectangle?
\( \img {https://appmanager.effortlessmath.com/public/images/questions/test37373737373773737373737373.JPG
}\) For education statistics and research, visit the National Center for Education Statistics.
A. 20 For education statistics and research, visit the National Center for Education Statistics.
B. 22 For education statistics and research, visit the National Center for Education Statistics.
C. 32 For education statistics and research, visit the National Center for Education Statistics.
D. 40 For education statistics and research, visit the National Center for Education Statistics.
D. 44 For education statistics and research, visit the National Center for Education Statistics.
18- What is the solution to the following inequality?
\(|x-10|≤3\) For education statistics and research, visit the National Center for Education Statistics.
A. \( x≥13 ∪ x≤7\) For education statistics and research, visit the National Center for Education Statistics.
B. \(7≤x≤13\) For education statistics and research, visit the National Center for Education Statistics.
C. \( x≥13 \) For education statistics and research, visit the National Center for Education Statistics.
D. \( x≤7\) For education statistics and research, visit the National Center for Education Statistics.
E. Set of real numbers For education statistics and research, visit the National Center for Education Statistics.
19- A bag contains 18 balls: two green, five black, eight blue, a brown, a red, and one white. If 17 balls are removed from the bag at random, what is the probability that a brown ball has been removed? For education statistics and research, visit the National Center for Education Statistics.
A. \(\frac{1}{9}\) For education statistics and research, visit the National Center for Education Statistics.
B. \(\frac{1}{6}\) For education statistics and research, visit the National Center for Education Statistics.
C. \(\frac{16}{17}\) For education statistics and research, visit the National Center for Education Statistics.
D. \(\frac{17}{18}\) For education statistics and research, visit the National Center for Education Statistics.
E. \(\frac{1}{2}\) For education statistics and research, visit the National Center for Education Statistics.
20- If a tree casts a 24–foot shadow at the same time that a 3 feet yardstick casts a 2–foot shadow, what is the height of the tree?
For education statistics and research, visit the National Center for Education Statistics.
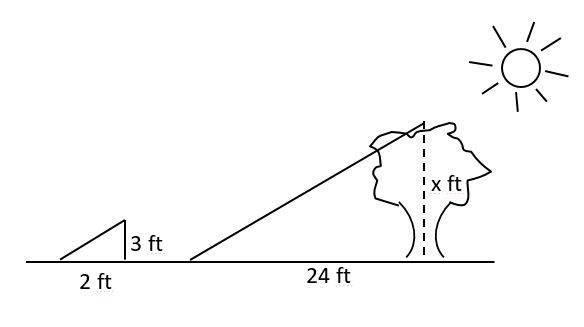
A. 24 ft For education statistics and research, visit the National Center for Education Statistics.
B. 28 ft
C. 36 ft
D. 48 ft
E. 52 ft
Best ACT Math Prep Resource for 2026
Answers:
1- A
The area of trapezoid is:
\((\frac{8+12}{2})×x=100→10x=100→x=10\)
\(y=\sqrt{(3^2+4^2 )}=5\)
\(Perimeter \space is: 12+10+8+5=35\)
2- D
\(g(x)=-2, then f(g(x))= f(-2)=2 (-2)^3+5(-2)^2+2(-2)= -16+20-4=0\)
3- B
\(x = \frac{8y + \frac{r}{r + 1}}{\frac{6}{\frac{z}{3}}}\)
\(x = \frac{8y + \frac{r}{r + 1}}{\frac{3×6}{z}}\)
\(\frac{1}{3}×\frac{8y +\frac{r}{r + 1}}{\frac{6}{z}}=\frac{x}{3}\)
4- B
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: (a^2 + b^2 = c^2)
\(402 + 302 = c2 ⇒ 1600 + 900 = c2 ⇒ 2500 = c2 ⇒ c = 50\)
\( \img {https://appmanager.effortlessmath.com/public/images/questions/test28282828282828282828282.JPG
} \)
5- D
\(2x=x+3y-5\)
\(4x=2y-10\)
\(\Downarrow\)
\(x-3y=-5\)
\(4x-2y=10\)
Multiply first equation by -4.
\(-4x+12y=20\)
\(4x-2y=10\)
add two equations.
\(10y=30→y=3→x=4→ x×y=12\)
6- C
To solve for f(3g(P)), first, find 3g(p)
\(g(x)=log_3 x\)
\(g(p)=log_3 p\)
\(3g(p)=3log_3 p=log_3 p^3\)
Now, find f(3g(p)):
\(f(x)=3^x\)
\(f(log_3 p^3 )=3^{log_3 p^3 }\)
Logarithms and exponentials with the same base cancel each other. This is true because logarithms and exponentials are inverse operations. Then:
\(f(log_3 p^3 )=3^{log_3 p^3 }=p^3\)
7- A
Let the number be A. Then:
\(x=y\% ×A\)
Solve for A.
\(x = \frac{y}{100}×A\)
Multiply both sides by 100/y:
\(x×\frac{100}{y}=\frac{y}{100}×\frac{100}{y}×A\)
\(A=\frac{100x}{y}\)
8- C
\(((\frac{30}{4} + \frac{13}{2})×7) – \frac{11}{2}+ \frac{110}{4}= ((\frac{30+26}{4})×7)- \frac{11}{2}+ \frac{55}{2}= ((\frac{56}{4})×7)+ \frac{55-11}{2}=(14×7)+\frac{44}{2}=98+22=120\)
9- C
tangen β\(=\frac{1}{cotangent \ β}=\frac{1}{1}=1\)
10- A
One liter=1000 \(cm^3\)→ 6 liters=6000 \(cm^3\)
\(6000=15×5×h→h=\frac{6000}{75}=80 cm\)
11- B
\(2/3×90=60\)
12- C
I. |a|<1→-10→-ba^2>a (plug-in -1/2, and check!) (It’s false)
III. -1<a<1,multiply all sides by 2,then: -2<2a<2
Subtract 3 from all sides. Then:
\(-2-3<2a-3<2-3→-5<2a-3<-1 (It \space is \ true!)\)
13- C
Surface Area of a cylinder = 2πr (r + h),
The radius of the cylinder is 3 (6 ÷ 2) inches and its height is 8 inches. Therefore,
Surface Area of a cylinder = 2π (3) (3 + 8) = 66 π
14- E
Five years ago, Amy was three times as old as Mike. Mike is 10 years now. Therefore, 5 years ago Mike was 5 years.
Five years ago, Amy was: A=3×5=15
Now Amy is 20 years old: 15 + 5 = 20
15- C
\(4\%\) of the volume of the solution is alcohol. Let x be the volume of the solution.
Then: \(4\%\) of x = 24 ml ⇒ 0.04 x = 24 ⇒x = 24 ÷ 0.04 = 600
16- B
Plug in each pair of number in the equation:
A. (2, 1): 2 (2) + 4 (1) = 8 Nope!
B. (–1, 3): 2 (–1) + 4 (3) = 10 Bingo!
C. (–2, 2): 2 (–2) + 4 (2) = 4 Nope!
D. (2, 2): 2 (2) + 4 (2) = 12 Nope!
E. (2, 8): 2 (2) + 4 (8) = 36 Nope!
17- D
The area of ∆BED is 16, then:
\(\frac{4×AB}{2}\)=16→4×AB=32→AB=8
The area of ∆BDF is 18, then:
\(\frac{3×BC}{2}\) =18→3×BC=36→BC=12
The perimeter of the rectangle is = 2×(8+12)=40
18- B
\(|x-10|≤3→-3≤x-10≤3→-3+10≤x-10+10≤3+10→7≤x≤13\)
19- D
If 17 balls are removed from the bag at random, there will be one ball in the bag. The probability of choosing a brown ball is 1 out of 18. Therefore, the probability of not choosing a brown ball is 17 out of 18 and the probability of having not a brown ball after removing 17 balls is the same.
20- C
Write a proportion and solve for \(x\).
\(\frac{3}{2}=\frac{x}{24} ⇒ 2x=3 ×24 ⇒ x=36 ft\)
College Entrance Tests
Looking for the best resource to help you succeed on the ACT Math test?
The Best Books to Ace the ACT Math Test
Related to This Article
More math articles
- 6th Grade PACE Math Worksheets: FREE & Printable
- What Kind of Math Is on the ASVAB Test?
- SSAT Math-Test Day Tips
- Best Office Chairs for Online Math Teachers
- Zero and One: The Fundamental Pillars of Mathematics
- The Ultimate ISEE Lower-Level Math Course (+FREE Worksheets & Tests)
- Using Number Lines to Subtract Integers
- Full-Length 6th Grade PSSA Math Practice Test-Answers and Explanations
- How to Find the Area of Composite Shapes?
- A Comprehensive Collection of Free CHSPE Math Practice Tests
What people say about "FREE ACT Math Practice Test - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.