How to Graph Rational Functions?

The general form of a rational function is \(\frac {p(x)}{q(x)}\), where \(p(x)\) and \(q(x)\) are polynomials and \(q(x) ≠ 0\).

Related Topics

• How to Graph Rational Expressions
• How to Add and Subtract Rational Expressions
• How to Multiply Rational Expressions
• How to Solve Rational Equations

A step-by-step guide to graphing rational functions

Each rational function may be graphed using the following steps:

1. Find the \(y\)-intercept by evaluating the function at zero.
2. Multiply the numerator and denominator together.
3. Determine where each numerator component is zero to discover the \(x\)-intercepts for factors in the numerator that are not common to the denominator.
4. Determine the behavior of the graph at those places by finding the multiplicities of the \(x\)-intercepts.
5. Note the multiplicities of the zeros in the denominator to determine the local behavior. Find the vertical asymptotes for those components that are not common to the numerator by setting them to zero and then solving them.
6. Find the removable discontinuities in the denominator that are similar to factors in the numerator by setting those factors to \(0\) and then solving.
7. To get the horizontal or slant asymptotes, compare the degree of the numerator and denominator.
8. Draw the graph.

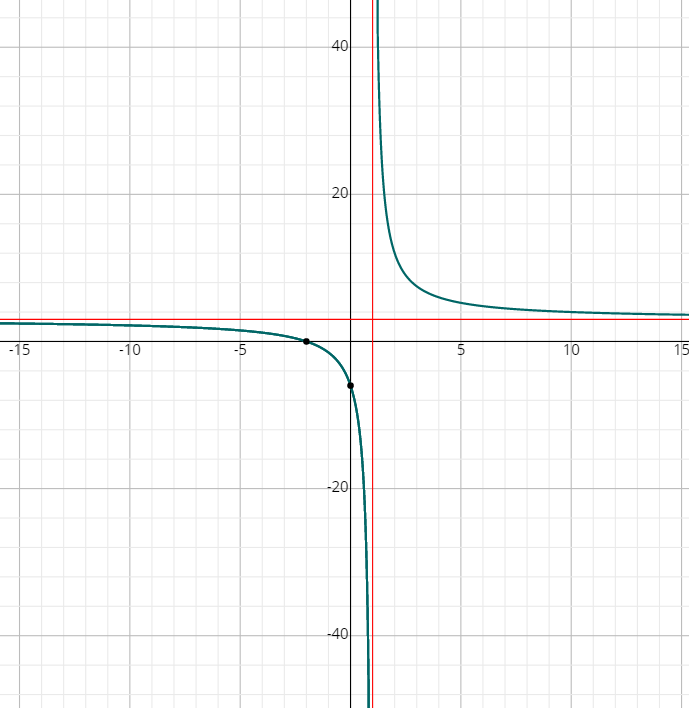
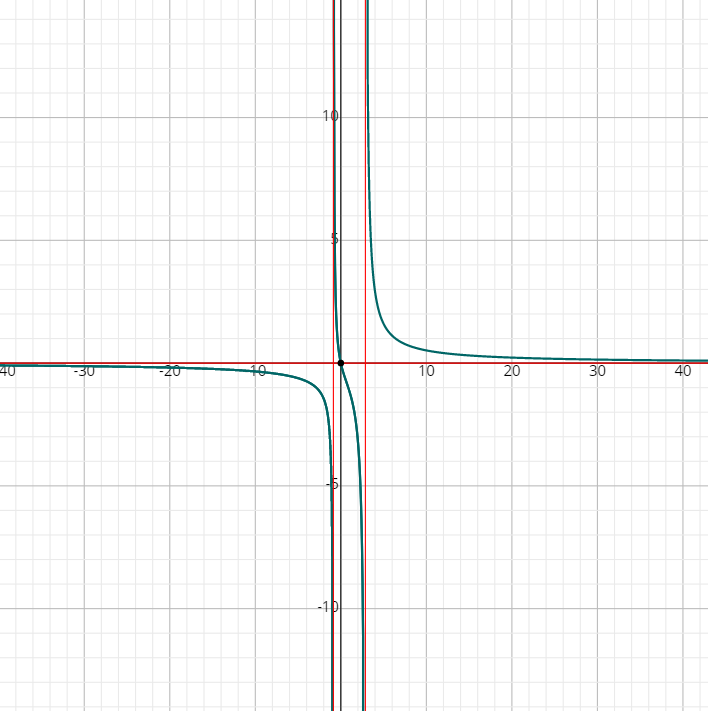
Graphing Rational Functions – Example 1:

Sketch the graph of the following function: \(f(?)=\frac{3?+6}{?−1}\)

First, find the \(y\)-intercept: \(f(0)=\frac{3(0)+6}{0−1}=\frac {6}{-1}=-6 → (0,-6)\)

Then, find the \(x\)-intercepts: \(3x+6=0 → 3x=-6 → x=\frac{-6}{3}=-2 → (-2,0)\)

Now, we have to determine the asymptotes:

Vertical asymptote: \(x=1\), Horizontal asymptote: \(?=3\)

Now, we only need points in each region of \(x\)’s. Since \(y\)-intercept and \(x\)-intercept is currently in the left region, we will not need to point there. This means that we need to get a point in the right region. It does not matter how much \(x\) we choose here; we just need to keep it relatively small to fit on our graph.

\(f(2)=\frac{3(2)+6}{2−1}=\frac{12}{1}=12\)

By putting all this together, the following diagram is obtained.

Exercises for Graphing Rational Functions

Graph these rational functions.

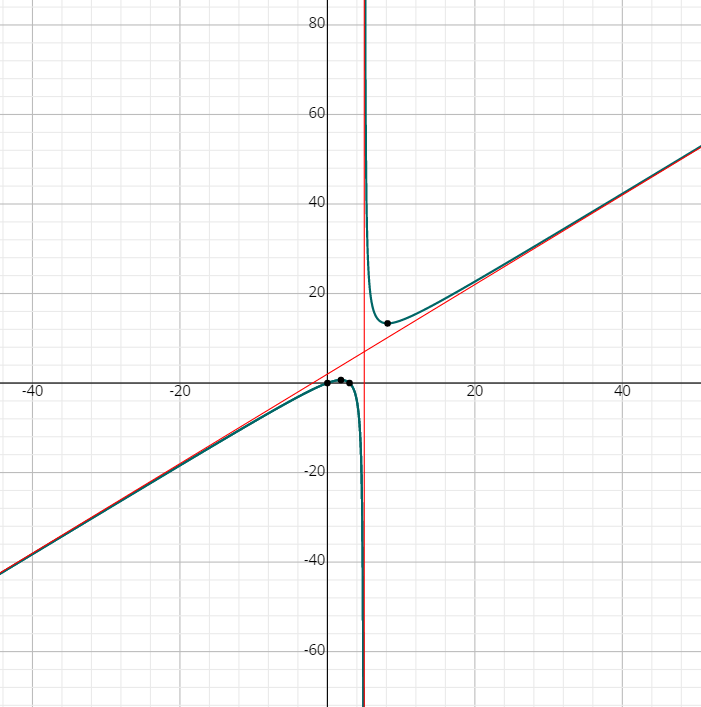
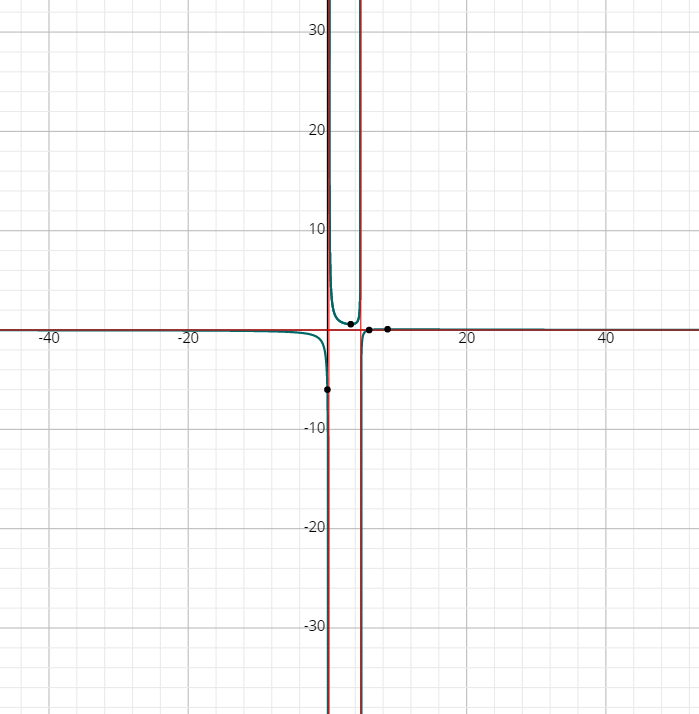
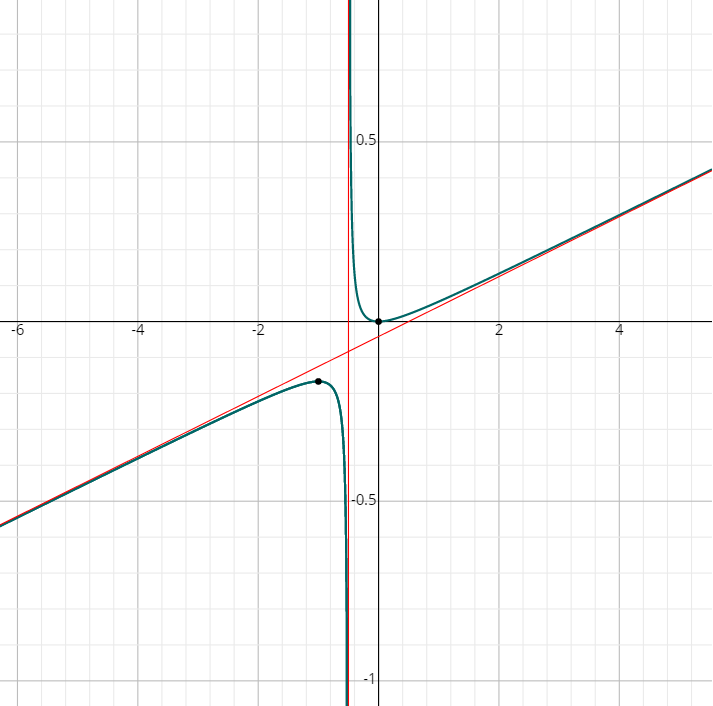
• \(\color{blue}{f(x)=\frac{x^2 -3x}{x-5}}\)

• \(\color{blue}{f(x)=\frac{x-6}{x^2-5x+1}}\)

• \(\color{blue}{f(x)=\frac{x^2}{12x+6}}\)

\(\color{blue}{f(x)=\frac{8x}{2x^2-4x-5}}\)

• \(\color{blue}{f(x)=\frac{x^2 -3x}{x-5}}\)

\(\color{blue}{f(x)=\frac{x-6}{x^2-5x+1}}\)

\(\color{blue}{f(x)=\frac{8x}{2x^2-4x-5}}\)