How to Graph Rational Expressions? (+FREE Worksheet!)
In this post, you will learn how to graph Rational Expressions. You can graph Rational Expressions in a few simple steps.
Related Topics
- How to Add and Subtract Rational Expressions
- How to Multiply Rational Expressions
- How to Divide Rational Expressions
- How to Solve Rational Equations
- How to Simplify Complex Fractions
A step-by-step guide to Graphing Rational Expressions
- A rational expression is a fraction in which the numerator and/or the denominator are polynomials. Examples: \(\frac{1}{x},\frac{x^2}{x-1},\frac{x^2-x+2}{x^2+5x+1},\frac{m^2+6m-5}{m-2m}\)
- To graph a rational function:
- Find the vertical asymptotes of the function if there are any. (Vertical asymptotes are vertical lines that correspond to the zeroes of the denominator. The graph will have a vertical asymptote at \(x=a\) if the denominator is zero at \(x=a\) and the numerator isn’t zero at \(x=a\))
- Find the horizontal or slant asymptote. (If the numerator has a bigger degree than the denominator, there will be a slant asymptote. To find the slant asymptote, divide the numerator by the denominator using either long division or synthetic division.)
- If the denominator has a bigger degree than the numerator, the horizontal asymptote is the \(x\)-axes or the line \(y=0\). If they have the same degree, the horizontal asymptote equals the leading coefficient (the coefficient of the largest exponent) of the numerator divided by the leading coefficient of the denominator.
- Find intercepts and plug in some values of \(x\) and solve for \(y\), then graph the function.
Examples
Graphing Rational Expressions – Example 1:
Graph rational function. \(f(x)=\frac{x^2-x+2}{x-1}\)
Solution:
First, notice that the graph is in two pieces. Most rational functions have graphs in multiple pieces. Find \(y\)-intercept by substituting zero for \(x\) and solving for \(y (f(x)): x=0→y=\frac{x^2-x+2}{x-1}=\frac{0^2-0+2}{0-1}=-2\),
\(y\)-intercept: \((0,-2)\)
Asymptotes of \(\frac{x^2-x+2}{x-1}\): Vertical: \(x=1\), Slant asymptote: \(y=x\)
After finding the asymptotes, you can plug in some values for \(x\) and solve for \(y\). Here is the sketch for this function.
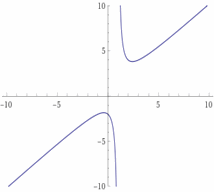
Best Algebra Prep Resource
Graphing Rational Expressions – Example 2:
Graph rational expressions. \(f(x)=\frac{3x}{x^2-2x}\)
Solution:
First, notice that the graph is in two pieces. Find \(y\)-intercept by substituting zero for \(x\) and solving for \(y (f(x)): x=0→y=\frac{3x}{x^2-2x}=\frac{3(0)}{(0^2-2(0)}=\frac{0}{0}\), \(y\)-intercept: None Asymptotes of \(\frac{3x}{x^2-2x}\): vertical: \(x=2\), Horizontal: \(y=0\) After finding the asymptotes, you can plug in some values for \(x\) and solve for \(y\). Here is the sketch for this function.
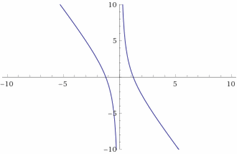
Exercises for Graphing Rational Expressions
Graph these rational expressions.
- \(\color{blue}{f(x)=\frac{x^2 -2x}{x-1}}\)
- \(\color{blue}{f(x)=\frac{x -5}{x^2-5x+1}}\)
- \(\color{blue}{f(x)=\frac{x^2}{4x-5}}\)
- \(\color{blue}{f(x)=\frac{5x-4}{2x^2-4x-5}}\)
- \(\color{blue}{f(x)=\frac{x^2 -2x}{x-1}}\)
- \(\color{blue}{f(x)=\frac{x -5}{x^2-5x+1}}\)
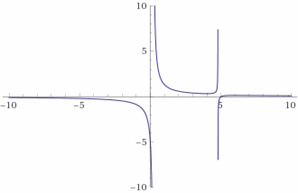
- \(\color{blue}{f(x)=\frac{x^2}{4x-5}}\)
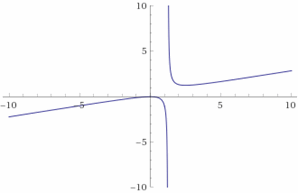
- \(\color{blue}{f(x)=\frac{5x-4}{2x^2-4x-5}}\)
The Absolute Best Book for the Algebra Test
Related to This Article
More math articles
- Exponential and logarithmic integrals Simplified
- How to Identify Statistical Questions
- 10 Most Common 8th Grade MAP Math Questions
- How to Remove Discontinuity from a Function
- GED Math FREE Sample Practice Questions
- Introduction to Sequences and Series: Fundamentals, Types, and Applications
- Quotient Quest: How to Master Division with Decimal Results
- How to Write Linear Equations From Y-Intercept and A Slope
- Top 10 Tips to Overcome ACT Math Anxiety
- How to Add and Subtract Integers? (+FREE Worksheet!)
What people say about "How to Graph Rational Expressions? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.