Full-Length GED Math Practice Test-Answers and Explanations

Did you take the GED Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.

GED Mathematical Reasoning Practice Test Answers and Explanations

1- Choice A is correct
Plug in the value of \(x\) and \(y\): \(2x(y-2x)+(2y-x)^2\) when \(x=-1\) and \(y=2⇒2(-1)(2-2(-1))+(2(2)-(-1))^2=-8+25=17\)

2- Choice C is correct
The equation of a line in slope intercept form is: \(y=mx+b\). Solve for \(y\).
\(-4x-y=8⇒y=-8-4x\). The slope of line is \(-4\). Therefore, the slope of a line that is perpendicular to this line is \(m^{‘}=-\frac{1}{m}=\frac{1}{4}\)

3- Choice B is correct
To solve absolute values equations, write two equations.
\( 2x-6\) can equal positive 12, or negative 12. Therefore, \(\begin{cases}-2x-4=-8 \\ -2x-4=8 \end{cases}\).
\(\begin{cases}-2x=-4 \\ -2x=12 \end{cases} ⇒?=\frac{−8}{−4}=2, ?=\frac{12}{−2}=−6\)
Find the product of solutions: \(2×(-6)=-12\)

4- Choice C is correct
A. \((2, -8) ⇒ 2(2)-3(-8)=28≠13 \)
B. \((-2, -3) ⇒2(-2)-3(-3)=5≠13 \)
C. \((2, -3) ⇒2(2)-3(-3)=13=13 \)
D. \((2,3) ⇒2(2)-3(3)=-5≠13\)

5- Answer is -27
Use PEMDAS (order of operation):\( -2×|-4|+3×(-2)-[10-6×(-7)]÷4=-8-6-13=-27\)

6- Choice D is correct
Use simple interest formula: I=prt
I = interest, p = principal, r = rate, t = time.
I=\((25000)(0.029)(3)=2175\)

7- Choice A is correct
Let x be all expenses, then \(\frac{23}{100} x=$575 →x=\frac{100×$575}{23}=$2500\)
He spent for his rent: \(\frac{34}{100}×$2500=$850\)

8- Choice B is correct
Write the numbers in order:\(4,12,15,19,21,25,34\). Median is the number in the middle. So, the median is 19. The range is \(34-4=30\)

9- Choice D is correct
To get a sum of 8 for two dice, we can get 5 different options: \((6, 2), (5, 3), (4, 4), (3, 5), (2, 6)\) To get a sum of 10 for two dice, we can get 3 different options: \((6, 4), (5, 5), (4, 6)\) Therefore, there are 8 options to get the sum of 8 or 10. Since, we have \(6 × 6 = 36\) total options, the probability of getting a sum of 5 and 3 is 8 out of 36 or \(\frac{8}{36}=\frac{2}{9}\).

10- Answer is 118
The area of the square is 870.25. Therefore, the side of the square is the square root of the area. \(\sqrt{870.25}=29.5\)
Four times the size of the square is the perimeter: \(4 × 29.5 = 118\)

The Absolute Best Book to Ace the GED Math Test

GED Math for Beginners 2024 The Ultimate Step by Step Guide to Preparing for the GED Math Test

Download

$28.99 $14.99

Rated 4.33 out of 5 based on 105 customer ratings

Satisfied 91 Students

11- Choice A is correct
The perimeter of the trapezoid is 42 cm.
Therefore, the missing side (height) is \(= 45 – 15 – 9 – 5 = 13\).
Area of a trapezoid: \(A = \frac{1}{2} h (b_1 + b_2) = \frac{1}{2} (13) (5 + 9) = 91\)

12- Answer is 4
Use formula of rectangle prism volume.
V = (length) (width) (height) \(⇒ 924 = (21) (11)\) (height) ⇒ height \(= 924 ÷ 231 = 4\)

13- Choice D is correct
Change the numbers to decimal and then compare.
\(38\%=0.38 , 0.52=0.52, \frac{1}{10}=0.1, \frac{2}{5}=0.4\) Therefore \(\frac{1}{10}<38\%<\frac{2}{5}<0.52\).

14- Choice A is correct
Use the formula of areas of circles.
Area \(= πr^2 ⇒ 36 π> πr^2⇒ 36 > r^2⇒ r < 6\)
The radius of the circle is less than 6. Let’s put 6 for the radius. Now, use the circumference formula: Circumference \(=2πr=2π (6)=12 π\)
Since the radius of the circle is less than 6. Then, the circumference of the circle must be less than \(12π\).

15- Choice D is correct
Volume of a box \(=\) length \(×\) width \(×\) height \(= 6 × 5.5 × 9 = 297\)

16- Choice C and D is correct
(If you selected 3 choices and 2 of them are correct, then you get one point. If you answered 2 or 3 choices and one of them is correct, you receive one point. If you selected more than 3 choices, you won’t get any point for this question.) First, find the sum of five numbers.
average \(= \frac{sum of terms }{number of terms} ⇒ 32 = \frac{sum of 5 numbers}{5} ⇒ \)sum of 5 numbers \(= 32 × 5 = 160 \)
The sum of 5 numbers is 160. If a sixth number that is greater than 50 is added to these numbers, then the sum of 6 numbers must be greater than 210.
\(160 + 50 = 210 \)
If the number was 50, then the average of the numbers is:
average \(=\frac{sum of terms }{number of terms}=\frac{210}{6}=35\)
Since the number is bigger than 50. Then, the average of six numbers must be greater than 35. Choices C and D are greater than 35.

17- Choice C is correct
If the length of the box is 45, then the width of the box is one-fifth of it, 9, and the height of the box is 4.5 (one second of the width). The volume of the box is: \(V \(=\) lwh \(= (45) (9) (4.5) = 1822.5\)

18- Choice B is correct
Write the equation and solve for \(B: 0.50 A = 0.80 B\), divide both sides by 0.80, then: \(\frac{0.50}{0.80} A = B\), therefore: \(B = 0.625 A\), and \(B\) is 0.625 times of \(A\) or it’s \(62.5\%\) of \(A\).

19- Choice B is correct
Plugin 95 for F and then solve for C.
C \(= \frac{5}{9} (F – 32) ⇒\) C \(= \frac{5}{9} (95 – 32) ⇒\) C \(= \frac{5}{9} (63) = 35\)

20- Choice A is correct
Use simple interest formula: =prt (I = interest,p = principal,r = rate,t = time).
I=\((75,00)(0.0325)(6)=1462.5\)

Best GED Math Prep Resource for 2022

The Most Comprehensive GED Math Preparation Bundle Includes GED Math Prep Books, Workbooks, and Practice Tests

Download

$76.99 $36.99

Rated 4.46 out of 5 based on 140 customer ratings

Satisfied 132 Students

21- Answer is 144
\(\frac{6^4}{3^2} =\frac{6×6×6×6}{3×3}=144\)

22- Choice B is correct
Use percent formula: part\(=\frac{percent}{100}×\)whole
\(57=\frac{percent}{100}×95 ⇒ 57=\frac{percent ×95}{100} ⇒\) multiply both sides by 100.
\(5700=\)percent\(×95\), divide both sides by 95. \(60=\)percent

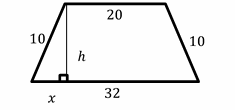
23- Choice D is correct
Area of a trapezoid: \(A = \frac{1}{2} h (b_1 + b_2)\). Therefore, the missing side is height(h). First, we should find \(x,h\)
\(x=\frac{32-20}{2}=4\). And \(10^2=x^2+h^2⇒h=\sqrt{10^2-x^2}\)
\(h=\sqrt{10^2-4^2}=\sqrt{64}=8\).
\(A=\frac{1}{2} h(b_1+b_2 )=\frac{1}{2}×8×(20+32)=208\)

24- Choice A is correct
Solving Systems of Equations by Elimination Add two equations.
\(\begin{cases}4x+2y=-9 \\ -2x-2y=-7 \end{cases} ⇒ 2x=-16 ⇒ x=-8 \)
Plug in the value of x into one of the equations and solve for \(y\).
\(4x+2y=-9⇒4(-8)+2y=-9⇒-32+2y=-9⇒2y=23⇒y=\frac{23}{2}\)

25- Choice B is correct
The equation of a line is in the form of \(y=mx+b\), where m is the slope of the line and b is the y-intercept of the line.
Two points \((1,0)\) and \((0,1)\) are on line A. Therefore, the slope of the line A is:
slope of line A\(=\frac{y_2- y_1}{x_2 – x_1} = \frac{1-0}{0-1}=\frac{1}{-1}=-1 \)
The slope of line A is \(-1\). Thus, the formula of the line A is: \(y=mx+b=-x+b\), choose a point and plug in the values of \(x\) and \(y\) in the equation to solve for b. Let’s choose point \((0, 1)\). Then:
\(y=x+b→1=0+b→b=1\)
The equation of line A is: \(y=-x+1\)
Now, let’s review the choices provided:
A.\((1,2) ⇒2=-1+1\). This is not true
B. \((-1,2)⇒2=1+1=2\). This is true
C. \((2,1)⇒1=-2+1=-1\). This is not true
D. \((3,1)⇒1=-3+1=-2\). This is not true

26- Choice A is correct
Use distance formula: Distance \(=\) Rate \(×\) time \(⇒ 540 = 75 ×\) T, divide both sides by \(\frac{75. 540 }{75} =\) T ⇒ T \(= 7.2\) hours.
Change hours to minutes for the decimal part. 0.2 hours \(= 0.2 × 60 = 12\) minutes

27- Choice D is correct
Let \(x\) be the number. Write the equation and solve for \(x\).
\(\frac{3}{5} ×22= \frac{3}{7}. x ⇒ \frac{3×22}{5}= \frac{3x}{7} \), use cross multiplication to solve for \(x\).
\(7×22=5x ⇒154=5x ⇒ x=30.8\)

28- Choice B is correct
To find the discount, multiply the number by (\(100\% –\) rate of discount).
Therefore, for the first discount we get: \((D) (100\% – 15\%) = (D) (0.85) = 0.85 D\)
For increase of \(10 \%: (0.85 D) (100\% + 10\%) = (0.85 D) (1.10) = 0.935 D = 93.5\%\) of \(D\)

29- Choice C is correct
Use the formula for Percent of Change: \(\frac{New Value-Old Value}{Old Value} × 100 \% \)
\(\frac{34-45}{45} × 100 \% = –24.44 \%\) (negative sign here means that the new price is less than old price).

30- Choices D and E are correct
(If you selected 3 choices and 2 of them are correct, then you get one point. If you answered 2 or 3 choices and one of them is correct, you receive one point. If you selected more than 3 choices, you won’t get any point for this question.) Some of the prime numbers are: \(2, 3, 5, 7, 11, 13\)
Find the product of two consecutive prime numbers:
\(2 × 3 = 6\) (not in the options)
\(3 × 5 = 15\) (Choice D)
\(5 × 7 = 35\) (Choice E)
\(7 × 11 = 77\) (not in the options)
Choices D and E are correct.

31- Answer is 249
The ratio of boys to girls is \(3:5\). Therefore, there are 3 boys out of 8 students. To find the answer, first, divide the total number of students by 8, then multiply the result by
\(3. 664 ÷ 8 = 83 ⇒ 83 × 3 = 249\)

32- Choice A is correct
The question is this: 440 is what percent of 550?
Use percent formula: part \(= \frac{percent}{100} ×\) whole
\(440 = \frac{percent}{100} × 550 ⇒ 440= \frac{percent ×550}{100} ⇒44000 =\) percent \(×550\) percent \(= \frac{44000}{550} = 80. 440\) is \(80 \%\) of 550. Therefore, the discount is: \(100\% – 80\% = 20\%\)

33- Choice B is correct
If the score of Mia was 48, therefore the score of Ava is 16. Since the score of Emma was half as that of Ava, therefore, the score of Emma is 8.

34- Choice A is correct
The sample space S of the experiment described is as follows:
\(S={(1,H),(2,H),(3,H),(4,H),(5,H),(6,H),(1,T),(2,T),(3,T),(4,T),(5,T),(6,T)} \)
Let E be the event “the die shows an odd number and the coin shows ahead”. Event E may be described as follows.
\(E={(1, H),(3,H),(5,H)}\)
The probability P(E) is given by P(E) \(= \frac{n(E)}{n(S)} = \frac{3 }{12} = \frac{1}{4}\)

35- Choice A is correct
Let \(x\) be the smallest number. Then, these are the numbers:
\(x, x+1, x+2, x+3, x+4\)
average \(= \frac{sum of terms}{number of terms} ⇒ = \frac{x+(x+1)+(x+2)+(x+3)+(x+4)}{5}⇒30=\frac{5x+10}{5} ⇒ 150=5x+10 ⇒ 140=5x ⇒ x=28\)

36- Choice D is correct
The area of the floor is: \(8\) cm \(× 20\) cm \(= 160\) cm\(^2\) The number of tiles needed \(= 160 ÷ 10 = 16\)

37- Choice B is correct
The weight of 9.6 meters of this rope is: \(9.6 × 500\)g \(= 4800\) g \(1\) kg \(= 1,000\) g, therefore, \(4800\) g \(÷ 1000 = 4.8\)kg

38- Choice B is correct
\(2.5\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution. Then:
\(2.5\%\) of \(x = 30\) ml \(⇒ 0.025 x = 30 ⇒ x = 30 ÷ 0.025 = 1200\) ml

39- Choice C is correct
average \(= \frac{sum of terms}{number of terms}\)
The sum of the weight of all girls is: \(15 × 62 = 930\) kg
The sum of the weight of all boys is: \(28 × 70 = 1960\) kg
The sum of the weight of all students is: \(930 + 1960 = 2890\) kg
average \(= \frac{2890}{43} = 67.21\)

40- Choice C is correct
Let \(x\) be the original price. If the price of a laptop is decreased by \(12\%\) to \($385\), then:
\(88 \%\) of \(x=385⇒ 0.88x=385 ⇒ x=385÷0.88=$437.5\)

41- Choice A is correct
Write the numbers in order: \(14,14,15,16,18,22,62\) Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 16.

42- Choice A is correct
Surface area of cone formula is : A\(=πr(r+\sqrt{h^2+r^2})\). For r\(=17\) and h\(=20\) A\(=π(17)(17+\sqrt{20^2+17^2} )≈2309.79\)

43- Choice D is correct
Let \(x\) be the number of years. Therefore, \($2,100\) per year equals \(2100x\).
starting from \($22,000\) annual salary means you should add that amount to \(2100x\).
Income more than that is: \(I > 2100x + 22000\)

44- Choice B is correct
The question is this: 1.65 is what percent of 1.05?
Use percent formula: part \(= \frac{percent}{100} ×\) whole
\(1.65 = \frac{percent}{100} × 1.05 ⇒ 1.65=\frac{percent ×1.05}{100} ⇒165=\)percent \(×1.05 ⇒\) percent\(=\frac{165}{1.05}=157\%\)

45- Choice D is correct
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(20^2 + 15^2 = c^2 ⇒ 400 + 225 = c^2 ⇒ 625 = c^2 ⇒ c = 25\)

46- Choice A is correct
For each option, choose a point in the solution part and check it on both inequalities.
\(y>2x ,y≥-x+2\)
A. Point \((0, 5)\) is in the solution section. Let’s check the point in both inequalities.
\(5>0\), It works
\(5≥0+2\), it works (this point works in both)
B. Let’s choose this point \((5, 0)\)
\(0>10\) That’s not true!
\(0≥-5+2\), it works
C. Let’s choose this point
\((–5, 0) 0>-10\), it works
\(0≥10+2\) That’s not true!
D. Let’s choose this point
\((0, 5) 5>0\), That’s not true!
\(5≥0+2\) it works

High School Equivalency Tests

The Best Books to Ace the GED Math Test

GED Math Test Prep The Ultimate to GED Math + 2 Full-Length Practice Tests

Download

$22.99 $14.99

Rated 4.34 out of 5 based on 107 customer ratings

Satisfied 94 Students

More from Effortless Math for GED Test …

Using the best prep book for your GED Math test is critical.

Find the best prep book for your GED Math test by reading our Top 10 GED Math Prep Books.

Want more guidance on how to prepare for your GED Math test?

Get tips on How to Prepare for GED Math Test.

The best way to study for the GED Math test is to use realistic GED Math practice questions.

Try our Free GED Math Practice Test to measure your exam readiness.

The Perfect Prep Books for the GED Math Test

GED Math Full Study Guide Comprehensive Review + Practice Tests + Online Resources

Download

$25.99 $13.99

Rated 4.49 out of 5 based on 134 customer ratings

Satisfied 125 Students

GED Math in 30 Days The Most Effective GED Math Crash Course

Download

$24.99 $14.99

Rated 4.41 out of 5 based on 221 customer ratings

Satisfied 207 Students

GED Math Practice Workbook 2024 The Most Comprehensive Review for the Math Section of the GED Test

Download

$27.99 $14.99

Rated 4.43 out of 5 based on 192 customer ratings

Satisfied 182 Students

Have any questions about the GED Test?

Write your questions about the GED or any other topics below and we’ll reply!