Full-Length ACT Math Practice Test

Taking a Full-length ACT Math practice test is the best way to help you get familiar with the test format and feel more confident. Not only will this help you measure your exam readiness and solidify the concepts you’ve learned, but it is the best way to simulate test day.
To help you get the best out of this complete and realistic ACT Math practice test and prepare your mind and body for the actual test, we recommend that you treat this practice test as a real test. Prepare scratch papers, a pencil, a timer, and a calculator and take the test in one sitting and follow the time limits to the minute.
Take the following full-length ACT Math practice test to simulate the test day experience. After you’ve finished, score your tests using the answer keys.
Good luck!

The Absolute Best Book to Ace the ACT Math Test

Time to refine your Math skill with a practice test

Best ACT Math Prep Resource for 2022

ACT Math Practice Test

60 questions
Total time for this section: 60 Minutes
You may use a scientific calculator on this test.

1- What is the median of these numbers? 10, 12, 14, 19, 23, 30, 32

A. 14

B. 19

C. 23

D. 30

E. 32

2- The number 5.08 is 1,000 times greater than which of the following numbers?

A. 50.8

B. 0.508

C. 0.0508

D.  0.00508

E.  0.000508

3- David’s current age is 25 years, and Ava’s current age is 8 years. In how many years David’s age will be 2 times Ava’s age?

A. 4

B. 6

C. 7

D. 9

E. 11

4- How many tiles of \(8.75\) \(cm^2\) is needed to cover a floor of dimension \(7 \space cm\) by \(20 \space cm\)?

A. 6

B. 12

C. 16

D. 24

E. 36

5- The marked price of a computer is D dollar. Its price decreased by \(18\%\) in January and later increased by \(12 \%\) in February. What is the final price of the computer in D dollars?

A. 0.8025 D

B. 0.8840 D

C. 0.9184 D

D. 1.218 D

E. 1.402 D

6- What is the value of \(y\) in the following system of equation?
\(5x-4y= -2\)
\(2x+2y= 10\)

A. \(-4\)

B. \(-2\)

C. \(1\)

D. \(3\)

E. \(5\)

7- What is the area of a square whose diagonal is \(15 \space cm\)?

A. \(16.5 \space cm^2\)

B. \(32.5 \space cm^2\)

C. \(36.5 \space cm^2\)

D. \(66.5 \space cm^2\)

E. \(112.5 \space cm^2\)

8- What is the value of \(x\) in the following figure?

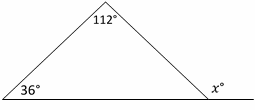
A. 32

B. 64

C. 140

D. 148

E. 152

9- Right triangle ABC is shown below. Which of the following is true for all possible values of angles A and B?

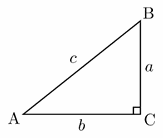
A. \(tan \space A = tan \space B\)

B. \(sin \space A = -cos \space B\)

C. \(tan^2 \space A=tan^2 \space B\)

D. \(tan \space A=1\)

E. \(cos⁡ \space A=sin \space B\)

10- A company pays its employer $11000 plus \(4\%\) of all sales profit. If \(x\) is the number of all sales profit, which of the following represents the employer’s revenue?

A. \(0.04x+11000\)

B. \(0.4x+11000\)

C. \(0.4x-11000\)

D. \(0.96x+11000\)

E. \(-0.96x-11000\)

11- What is the solution to the following inequality?
\(|x+8|≤5\)

A. \(x≥13 ∪ x≤7\)

B. \(7≤x≤13\)

C. \(x≥13\)

D. \(x≤13\)

E. \(-13≤x≤-3\)

12- From the figure, which of the following must be \(x\)?

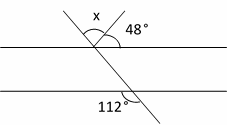
A. 52

B. 64

C. 72

D.  83

E.  90

13- Which is the correct statement?

A. \(\frac{1}{6} > 0.2\)

B. \(60\% = \frac{3}{5}\)

C. \(2.5 > \frac{10}{3}\)

D. \(\frac{5}{6} < 0.8\)

E. None of the above

14- When \(20\%\) of 120 is added to \(15\%\) of 300, the resulting number is:

A. 69

B. 72

C. 96

D. 140

E. 180

15- How long does a 600–miles trip take moving at 48 miles per hour (mph)?

A. 4 hours

B. 5 hours and 30 minutes

C. 8 hours and 30 minutes

D. 12 hours and 30 minutes

E. 13 hours and 30 minutes

16- \(8^{\frac{9}{2}} × 8^{\frac{5}{2}} =\)

A. \(8^0\)

B. \(8^1\)

C. \(8^3\)

D. \(8^5\)

E. \(8^7\)

17- If a tree casts a 30–foot shadow at the same time that a 4 feet yardstick casts a 3–foot shadow, what is the height of the tree?

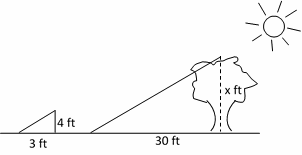
A. 24 ft

B. 28 ft

C. 36 ft

D. 40 ft

E. 52 ft

18- A ladder leans against a wall forming a \(60^\circ\) angle between the ground and the ladder. If the bottom of the ladder is 20 feet away from the wall, how long is the ladder?

A. 30 feet

B. 40 feet

C. 50 feet

D. 60 feet

E. 120 feet

19- If \(45\%\) of a class are girls, and \(30\%\) of girls play tennis, what percent of the class play tennis?

A. \(7\%\)

B. \(8.5\%\)

C. \(9\%\)

D. \(11.5\%\)

E. \(13.5\%\)

20- Jake is going to call one person from his contacts at random. He has 45 total contacts. 20 of those contacts are people he met at school. What is the probability Jake calls a person from school?

A. \(\frac{1}{9}\)

B. \(\frac{1}{6}\)

C. \(\frac{4}{9}\)

D. \(\frac{17}{18}\)

E. \(2.5\)

21- If a box contains red and blue balls in the ratio of 3: 7, how many red balls are there if 42 blue balls are in the box?

A. 12

B. 14

C. 16

D. 18

E. 20

22- In five successive hours, a car travels 24 km, 33 km, 52 km, 45 km, and 46 km. In the next five hours, it travels with an average speed of 45 km per hour. Find the total distance the car traveled in 10 hours.

A. 425 km

B. 450 km

C. 475 km

D. 500 km

E. 1,000 km

23- From last year, the price of gasoline has increased from $1.2 per gallon to $1.5 per gallon. The new price is what percent of the original price?

A. \(72 \%\)

B. \(125 \%\)

C. \(140 \%\)

D. \(155 \%\)

E. \(180 \%\)

24- 10.24 liters of water are poured into an aquarium that’s 32 cm long, 12 cm wide, and 40 cm high. How many cm will the water level in the aquarium rise due to this added water? (1 liter of water = 1000 \(cm^3\))

A. 22

B. 28

C. 32

D. 35

E. 45

25- Simplify.
\(3x^2+5y^2-4y^3-7z^2-3x^2+3x-5y^3+7z^2\)

A. \(3x^2-2y^2+y^3+7z^2\)

B. \(3x+2x^2-2y^2+y^3+7z^2\)

C. \(x+2x^2+3y^3+7z^2\)

D. \(x^2+2x-2y^2+7z^2\)

E. \(3x+5y^2-9y^3\)

26- If \(x\) is a real number, and if \(2x^3-40=210\), then what is \(x\) number?

A. 5

B. 6

C. 7

D. 8

E. 9

27- What is the surface area of the cylinder below?

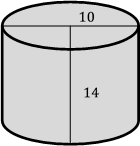
A. \(190 \space π \space in^2\)

B. \(210 \space π \space in^2\)

C. \(220 \space π \space in^2\)

D. \(230 \space π \space in^2\)

E. \(240 \space π \space in^2\)

28- Five years ago, Amy was four times as old as Mike was. If Mike is 12 years old now, how old is Amy?

A. 23

B. 28

C. 33

D. 35

E. 40

29- A chemical solution contains \(7\%\) alcohol. If there are 35 ml of alcohol, what is the volume of the solution?

A. 240 ml

B. 320 ml

C. 450 ml

D. 500 ml

E. 600 ml

30- If \(|a|<0.5\), then which of the following is true? (\(b>0\))?
I. \(–0.5b<ba <0.5b\)
II. \(-a>a^2>a \space if \space a<0\)
III. \(-3.5<3a-2<-0.5\)

A. I only

B. II only

C. I and III only

D. III only

E. I, II and III

31- Which of the following has the same period and three times the amplitude of graph \(y = cos x\)?

A. \(y=cos 2x\)

B. \(y=cos (x+2)\)

C. \(y=4 cos⁡2x\)

D. \(y=2+2 cos x\)

E. \(y=5+3cos x\)

32- If \((x-4)^3=64\) which of the following could be the value of \((x+2)(x-8)\)?

A. \(-2\)

B. \(-1\)

C. \(0\)

D.  \(1\)

E. \(2\) 

33- Simplify \(\frac{(-3+4i)}{(1-3i)}\)

A. \(-\frac{3}{2}-\frac{1}{2} i\)

B. \(-\frac{3}{2}+\frac{1}{2}i\)

C. \(-6-2i\)

D. \(-6+ 2i\)

E. \(6+2i\)

34- If \(tan \space \theta = \frac{4}{9}\) and \(sin \space \theta > 0\), then \(cos \space \theta =\) ?

A. \(-\frac{12}{13}\)

B. \(-\frac{5}{13}\)

C. \(\frac{5}{\sqrt{45}}\)

D. \(\frac{8}{\sqrt{88}}\)

E. \(\frac{9}{\sqrt{97}}\)

35- If \(\frac{10x}{12}=\frac{2x-1}{3}\), \(x=\)

A. \(-4\)

B. \(-2\)

C. \(3\)

D. \(4\)

E. \(5\)

36- Which of the following shows the numbers in increasing order?

A. \(\frac{4}{3},\frac{5}{8},\frac{3}{7},\frac{9}{15}\)

B. \(\frac{5}{8},\frac{3}{7}, \frac{4}{3}, \frac{9}{15}\)

C. \(\frac{5}{8}, \frac{4}{3}, \frac{9}{15}, \frac{3}{7}\)

D. \(\frac{3}{7},\frac{9}{15}, \frac{5}{8},\frac{4}{3}\)

E. None of them above

Questions 37 to 39 are based on the following data

The result of the research shows the number of men and women in four cities of a country.

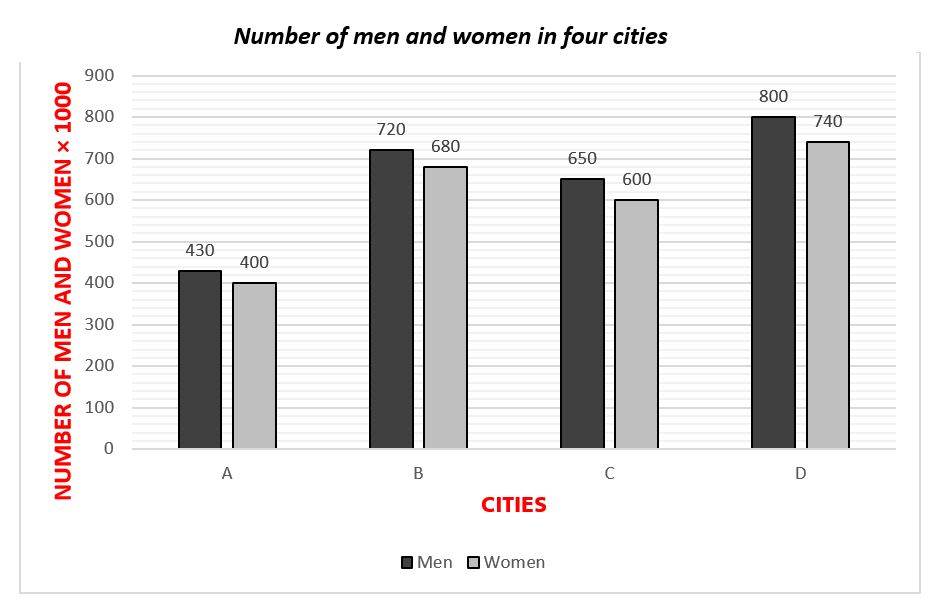
37- What’s the maximum ratio of the number of women to the number of men in each city?

A. 0.94

B. 0.95

C. 0.96

D. 0.97

E. 0.98

38- What’s the ratio of the percentage of men in city B to a percentage of women in city D?

A. \(\frac{19}{20}\)

B. \(\frac{20}{19}\)

C. \(\frac{9}{10}\)

D. \(\frac{10}{9}\)

E. \(1.07\)

39- How many women should be added to city C to change the ratio of women to men to 1.3?

A. 245

B. 255

C. 265

D. 275

E. 285

40- A boat sails 50 km south and then 120 km east. How far is the boat from its start point?

A. 100 km

B. 130 km

C. 140 km

D. 170 km

E. 200 km

41- What are the values of mode and median in the following set of numbers? \(22,12,18,14,14,36,44,52\)

A. Mode: 14 Median: 20

B. Mode: 14, 12 Median: 22

C. Mode: 12 Median: 20

D. Mode: 14 Median: 22

E. Mode: 14, Median: 30

42- If \(20\%\) of \(x\) equal to \(5\%\) of \(60\), then what is the value of \((x-3)^2\)?

A. 96

B. 100

C. 124

D.  144

E.  152

43- In the \(xy\)-plane, the point \((5,-1)\) and \((2,2)\) are on line A. Which of the following equations of lines is parallel to line A?

A. \(y=3x\)

B. \(y=10-x\)

C. \(y=\frac{x}{2}\)

D. \(y=2x\)

E. \(y=x\)

44- In the following equation when \(z\) is divided by 10, what is the effect on \(x\)? \(x=\frac{2y+\frac{2r}{r+1}}{\frac{5}{z}}\)

A. \(x\) is divided by 15

B. \(x\) is divided by 5

C. \(x\) does not change

D. \(x\) is divided by 10

E. \(x\) is multiplied by 10

45- In 1999, the average worker’s income increased $3,000 per year starting from a $15,000 annual salary. Which equation represents income greater than average? (I = income, \(x\) = number of years after 1999)

A. \(I< 3000 x + 15000\)

B. \(I > 3000 x- 15000\)

C. \(I > 3000 x + 15000\)

D. \(I< 3000 x- 15000\)

E. \(I > -3000 x + 15000\)

46- A rope weighs 400 grams per meter in length. What is the weight in kilograms of 25 meters of this rope? (1 kilograms = 1000 grams)

A. 0.010

B. 0.10

C. 1.00

D. 10.00

E. 100.0

47- If \(f(x)=5^x\) and \(g(x)=log_5 x\), which of the following expressions is equal to \(f(4g(p))\)?

A. \(3P\)

B. \(3^p\)

C. \(p^3\)

D. \(p^4\)

E. \(\frac{p}{3}\)

48- A number is chosen at random from 5 to 25. Find the probability of not selecting a composite number.

A. \(\frac{7}{20}\)

B. \(\frac{13}{10}\)

C. \(1\)

D. \(2\)

E. \(5\)

49- Removing which of the following numbers will change the average of the numbers to 7?
\(4,6,9,7,9,10\)

A. 4

B. 6

C. 7

D. 9

E. 10

50- If \(x\begin{bmatrix}5 & 0 \\0 & 2 \end{bmatrix}=\begin{bmatrix}2x+y-2 & 0 \\0 & 2y+4 \end{bmatrix}\), what is the product of \(?\) and \(?\)?

A. 8

B. 9

C. 10

D. 11

E. 12

51- If the cotangent of an angle \(β\) is 2, then the tangent of angle \(β\) is

A. \(-1\)

B. \(0\)

C. \(\frac{1}{2}\)

D. \(2\)

E. \(3\)

52- If \(f(x)=4x-3\) and \(g(x)=x^2-2x+6\) then find \((g+ f)(x)\)?

A. \(x^2 – 3x – 6\)

B. \(x^2 – 3x + 6\)

C. \(x^2+2x+3\)

D. \(–x^2 – 3x – 6\)

E. \(–x^2 + 3x – 6\) 

53- \(10x\) is \(y\%\) of what number?

A. \(\frac{100x}{y}\)

B. \(\frac{100y}{x}\)

C. \(\frac{x}{1,000y}\)

D. \(\frac{1,000x}{y}\)

E. \(\frac{xy}{1,000}\)

54- \(157\) is equal to

A. \(20-(4×10)+(6×30)\)

B. \(((\frac{25}{2}+\frac{30}{4})×(\frac{32}{4}))-\frac{8}{5}+\frac{46}{10}\)

C. \((\frac{11}{8}×72)+(\frac{125}{5})\)

D. \((2×10)+(50×1.5)+15\)

E. \(\frac{481}{6}+\frac{121}{3}\)

55- If \(y = 8ab -5b^3\), what is \(y\) when \(a = 6\) and \(b = -2\)?

A. \(-56\)

B. \(-22\)

C. \(0\)

D. \(12\)

E. \(45\)

56- If the area of a trapezoid is 150, what is the perimeter of the trapezoid?

A. 25

B. 50

C. 63

D. 72

E. 83

57- In the following figure, ABCD is a rectangle, and E and F are points on AD and DC, respectively. The area of ∆BED is 20, and the area of ∆BDF is 32. What is the perimeter of the rectangle?

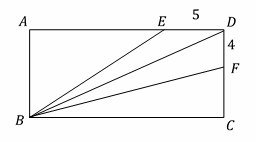
A. 20

B. 22

C. 32

D. 40

E. 48

58- When pointing A \((-6.-12)\) is reflected over the \(y\)-axis to get point B, what are the coordinates of point B?

A. \((6,- 12)\)

B. \((6,12)\)

C. \((-12,6)\)

D. \((12,-6)\)

E. \((-6,12)\)

59- Which of the following points lies on the line?
\(5x+3y=6\)

A. \((6, 1)\)

B. \((–3, 3)\)

C. \((3,-3)\)

D. \((2, 2)\)

E. \((2, 8)\)

60- If \(f(x)=2x^3+4x-18x^(-2)\) and \(g(x)=-3\), what is the value of \(f(g(x))\)?

A. \(-83\)

B. \(-68\)

C. \(-25\)

D. \(-13\)

E. \(0\)

College Entrance Tests

Answers and Explanations

The Best Books to Ace the ACT Math Test

More from Effortless Math for ACT Test …

Are you looking for a FREE ACT Math course to help you prepare for your test?

Check out our Ultimate ACT Math Course.

Need Math worksheets to help you measure your exam readiness for your upcoming ACT test?

Have a look at our comprehensive ACT Math Worksheets to help you practice and prepare for the ACT Math test.

Want to review the most common ACT Math formula?

Here is our complete list of ACT Math formulas.

The Perfect Prep Books for the ACT Math Test

Have any questions about the ACT Test?

Write your questions about the ACT or any other topics below and we’ll reply!