Full-Length ACT Math Practice Test-Answers and Explanations

Did you take the ACT Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.

ACT Math Practice Test Answers and Explanations

1- Choice B is correct
Write the numbers in order: 10, 12, 14, 19, 23, 30, 32
Since we have 7 numbers (7 is odd), then the median is the number in the middle, which is 19.

2- Choice D is correct.
1,000 times the number is 5.08. Let \(x\) be the number, then: \(1,000x=5.08\), \(x=\frac{5.08}{1,000}=0.00508\)

3- Choice D is correct.
Let’s review the options provided.
4. In 4 years, David will be 29 and Ava will be 12. 29 is not 2 times 12.
6. In 6 years, David will be 31 and Ava will be 14. 31 is not 2 times 14!
8. In 7 years, David will be 32 and Ava will be 15. 32 is not 2 times 15.
10. In 9 years, David will be 34 and Ava will be 17. 34 is 2 times 17.
14. In 11 years, David will be 36 and Ava will be 19. 36 is not 2 times 19.

4- Choice C is correct
The area of the floor is: 7 cm \(×\) 20 cm = 140 cm, The number is tiles needed \(= 140 ÷ 8.75 = 16\)

5- Choice C is correct
To find the discount, multiply the number by (\(100\%\) – rate of discount).
Therefore, for the first discount we get: \((D)(100\% – 18\%) = (D) (0.82) = 0.82 D\)
For increase of \(12\%\): \((0.82 D) (100\% + 12\%) = (0.82 D) (1.12) = 0.9184 D = 91.84\%\) of \(D\)

6- Choice D is correct
Solve the system of equations by elimination method.
\(\begin{cases}5x-4y= -2\\2x+2y=10\end{cases}\)
Multiply the second equation by \(2\), then add it to the first equation.
\(\begin{cases}5x-4y= -2\\2(2x+2y=10)\end{cases} ⇒\begin{cases}5x-4y= -2\\4x+4y=20\end{cases}\)
⇒ add the equations \(9x=18⇒x=2\).Replace \(x\) to one of equations. \(2x+2y=10→2(2)+2y=10→2y=6→y=3\)

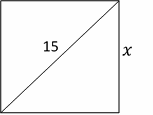
7- Choice E is correct
The diagonal of the square is 15. Let \(x\) be the side.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(x^2 + x^2 = 152 ⇒ 2x^2 = 152 ⇒ 2x^2 = 225 ⇒x^2 = 112.5 ⇒x= \sqrt{112.5}\)
The area of the square is: \(\sqrt{112.5} × \sqrt{112.5} = 112.5\)

8- Choice D is correct
\(x=36+112=148\)

9- Choice E is correct.
By definition, the sine of an acute angle is equal to the cosine of its complement.
Since angle A and B are complementary angles, therefore: sin A = cos B

10- Choice A is correct
Employer’s revenue: \(0.04x+11000\)

11- Choice E is correct
\(|x+8|≤5→-5≤x+8≤5→-13≤x≤-3\)

12- Choice B is correct
According to picture \(x+48=112→x=112-48=64\)

13- Choice B is correct
Check each option.
A. \(\frac{1}{6}> 0.2→ \frac{1}{6}=0.16\) and it is less than \(0.2\). Not true!
B. \(60\% = \frac{3}{5} → 60\% = \frac{3}{5}=0.6\). True!
C. \(2.5 > \frac{10}{3} → \frac{10}{3} =3.33\) and it is greater than \(2.5\). Not True!
D. \(\frac{5}{6}< 0.8 → \frac{5}{6}=0.8333…\) and it is greater than \(0.8\). Not True!
E. None of them above → Not True!

14- Choice A is correct
\(20\%\) of 120 equals to: \(0.20×120=24\), \(15\%\) of 300 equals to: \(0.15×300=45\)
\(20\%\) of 120 is added to \(15\%\) of 300: \(24+45=69\)

15- Choice D is correct
Use distance formula: Distance = Rate × time ⇒ 600 = 48 \(×\) T, divide both sides by 48. \(\frac{600}{48}\) = T ⇒ T = 12.5 hours. Change hours to minutes for the decimal part. 0.5 hours \(= 0.5 × 60 = 30\) minutes.

16- Choice A is correct
\(8^{\frac{9}{2}} × 8^{\frac{5}{2}} = 8^{\frac{9}{2} + \frac{5}{2}} = 8^{\frac{14}{2}} = 8^7\)

17- Choice D is correct
Write a proportion and solve for \(x\). ⇒ \(\frac{4}{3}=\frac{x}{30} ⇒ 3x=4 ×30 ⇒ x=40 \space ft\)

18- Choice B is correct
The relationship among all sides of the special right triangle
\(30^\circ -60^\circ – 90^\circ\) is provided in this triangle:

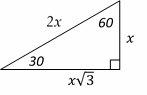
In this triangle, the opposite side of \(30^\circ\) angle is half of the hypotenuse.
Draw the shape of this question:

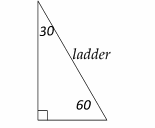
The ladder is the hypotenuse. Therefore, the ladder is 40 ft.

19- Choice E is correct
The percent of girls playing tennis is: \(45 \% × 30 \% = 0.45 × 0.30 = 0.135 = 13.5 \%\)

20- Choice C is correct
Probability \(= \frac{Number \space of \space favorable \space outcomes}{Number \space of \space possible \space outcomes}=\frac{20}{45}=\frac{4}{9}\)

The Absolute Best Book to Ace the ACT Math Test

ACT Math for Beginners 2023 The Ultimate Step by Step Guide to Preparing for the ACT Math Test

Download

$24.99 $14.99

Rated 4.43 out of 5 based on 54 customer ratings

Satisfied 46 Students

21- Choice D is correct
\(\frac{3}{7}×42=18\)

22- Choice A is correct
Add the first 5 numbers. \(24 + 33 + 52 + 45 + 46 = 200\)
To find the distance traveled in the next 5 hours, multiply the average by number of hours.
Distance = Average \(×\) Rate \(= 45 × 5 = 225\), Add both numbers. \(200 + 225 = 425\)

23- Choice B is correct
The question is this: 1.5 is what percent of 1.2? Use percent formula: \(part = \frac{percent}{100}× whole\)
\(1.5= \frac{percent}{100} × 1.2 ⇒ 1.5 =\frac{percent ×1.2}{100} ⇒150 = percent ×1.2 ⇒ percent = \frac{150}{1.2} = 125\)

24- Choice C is correct
\(One \space liter=1,000 \space cm^3→ 10.24 \space liters=10,240 \space cm^3\)⇒ \(10,240=32×10×h→h=\frac{10240}{320}=32 \space cm\)

25- Choice E is correct
\(3x^2+5y^2-4y^3-7z^2-3x^2+3x-5y^3+7z^2=3x^2-3x^2+3x+5y^2-4y^3-5y^3-7z^2+7z^2=3x+5y^2-9y^3\)

26- Choice A is correct
Solve for \(x\)→\(2x^3-40=210→x^3=125→x=5\)

27- Choice A is correct
Surface Area of a cylinder \(= 2πr (r + h)\), The radius of the cylinder is \(5 (10 ÷ 2)\) inches and its height is 14 inches. Therefore, Surface Area of a cylinder \(= 2π (5) (5 + 14) = 190 π\)

28- Choice C is correct
Five years ago, Amy was four times as old as Mike. Mike is 12 years now. Therefore, 5 years ago Mike was 7 years. Five years ago, Amy was: A\(=4×7=28\) , Now Amy is 33 years old:\( 28 + 5 = 33\)

29- Choice D is correct
\(7\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(7\%\) of \(x =35\) ml ⇒ \(0.07 x = 35 ⇒ x = 35 ÷ 0.07 = 500\)

30- Choice C is correct
I. \(|a|<0.5→-0.5<a<0.5\), Multiply all sides by b. Since, \(b>0→-0.5b<ba<0.5b\) (it is true!)
II. Since, \(-0.5<a<0.5,\) and \(a<0 →-a(0.5)>a^2>a(0.5)\) (plug in \(-\frac{1}{3}\), and check!) (It’s NOT true)
III. \(-0.5<a<0.5\), multiply all sides by \(3\), then: \(-1.5<3a<1.5\)
Subtract 2 from all sides. Then: \(-1.5-2<3a-2<1.5-2→-3.5<3a-2<-0.5\) (It is true!)

31- Choice E is correct
The amplitude in the graph of the equation \(y=acosbx\) is \(a\). (\(a\) and \(b\) are constant)
In the equation \(y=cosx\), the amplitude is 3 and the period of the graph is \(2π\).
The only option that has three times the amplitude of graph \(y = cos x\) is \(y=5+3 \space cos x\)
They both have the amplitude of 3 and period of \(2π\).

32- Choice C is correct
\((x-4)^3=64→x-4=4→x=8, →(x+2)(x-8)=(8+2)(8-8)=0\)

33- Choice A is correct
We know that: \(i=\sqrt{-1}⇒i^2=-1\)
\(\frac{-3+4i}{1-3i}=\frac{(-3+4i)(1+3i)}{1-9i^2 }
=\frac{-3-9i+4i+12i^2}{10}=\frac{-15}{10}-\frac{5}{10} i=-\frac{3}{2}-\frac{1}{2} i\)

34- Choice E is correct
\(tan=\frac{opposite}{adjacent}\),
\(tanθ=\frac{4}{9}\)⇒ we have the following right triangle.

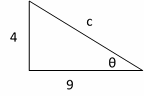
Then: \(c=\sqrt{4^2+9^2}=\sqrt{16+81}=\sqrt{97}\)
\(cosθ=\frac{adjacent}{hypotenuse}=\frac{9}{\sqrt{97}}\)

35- Choice B is correct.
Solve for \(x\).
\(\frac{10x}{12}=\frac{2x-1}{3}\). Multiply the second fraction by 4.
\(\frac{10x}{12}=\frac{4(2x-1)}{4×3}\)
Two denominators are equal. Therefore, the numerators must be equal.
\(10x=8x-4,2x=-4, -2=x\)

36- Choice D is correct
\(\frac{4}{3}≅1.33\), \(\frac{5}{8}≅0.625\), \(\frac{3}{7}≅0.43\), \(\frac{9}{15}=0.6\)

37- Choice A is correct
ratio of A: \(\frac{400}{430}=0.93\)
ratio of B: \(\frac{680}{720}=0.94\)
ratio of C: \(\frac{600}{650}=0.93\)
ratio of D: \(\frac{740}{800}=0.925\)

38- Choice E is correct
First find percentage of men in city B and percentage of women in city D.
Percentage of men in city B \(=\frac{720}{1,400}\) and percentage of women in city D \(=\frac{740}{1,540}\)
Find the ratio and simplify. \(\frac{\frac{720}{1,400}}{\frac{740}{1,540}}=\frac{198}{185}=1.07\)

39- Choice A is correct
\(\frac{600+x}{650}=1.3→600+x=845→x=245\)

40- Choice B is correct
Use the information provided in the question to draw the shape. Use Pythagorean Theorem:

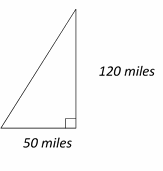
\(a^2 + b^2 = c^2⇒ 50 + 120 = c^2 ⇒ 2500 + 14400 = c^2 ⇒ 16900 = c^2 ⇒ c = 130 \space km\)

Best ACT Math Prep Resource for 2022

The Most Comprehensive ACT Math Preparation Bundle Includes ACT Math Prep Books, Workbooks, and Practice Tests

Download

$76.99 $36.99

Rated 4.35 out of 5 based on 153 customer ratings

Satisfied 138 Students

41- Choice A is correct
We write the numbers in the order: 12, 14, 14, 18, 22, 36, 44, 52
The mode of numbers is: 14 median is: 20

42- Choice D is correct
\(0.2x=(0.05)×60→x=15→(x-3)^2=(12)^2=144\)

43- Choice B is correct
The slop of line A is: \(m=\frac{y_2-y_1}{x_2-x_1}=\frac{2-(-1)}{2-5}=-1\)
Parallel lines have the same slope and only choice E \((y=-x)\) has slope of \(-1\).

44- Choice D is correct
Replace \(z\) by \(\frac{z}{10}\) and simplify.
\(x_1=\frac{2y+\frac{2r}{r+1}}{\frac{5}{\frac{z}{10}}}=
\frac{2y+\frac{2r}{r+1}}{\frac{10×5}{z}}
=\frac{2y+\frac{2r}{r+1}}{10×\frac{5}{z}}=\frac{1}{10}×\frac{2y+\frac{2r}{r+1}}{\frac{5}{z}}=\frac{x}{10}\)
When \(z\) is divided by 10, \(x\) is also divided by 10.

45- Choice C is correct
Let \(x\) be the number of years. Therefore, \($3,000\) per year equals \(3,000x\).
starting from \($15,000\) annual salary means you should add that amount to \(3,000x\).
Income more than that is: \(I > 3,000 x + 15,000\)

46- Choice D is correct
The weight of 25 meters of this rope is: 25 × 400 g = 10,000 g
1 kg = 1,000 g, therefore, 10,000 g ÷ 1,000 = 10 kg

47- Choice D is correct.
To solve for \(f(4g(P))\), first, find \(4g(p)\)
\(g(x)=log_5 x, g(p)=log_5 p, 4g(p)=4log_5 p=log_5 p^4\)
Now, find \(f(4g(p))\): \(f(x)=5^x⇒f(log_5 p^4 )=5^{log_5 p^4 }\)
Logarithms and exponential with the same base cancel each other. This is true because logarithms and exponential are inverse operations. Then: \(f(log_5 p^4 )=5^{log_5 p^4 }=p^4\)

48- Choice A is correct
Set of number that are not composite between 5 and 25: A= { 5, 7, 11, 13, 17, 19, 23}
Probability \(= \frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}=\frac{7}{20}\)

49- Choice E is correct
Check each choice provided:
A. \(4→ \frac{6+9+7+9+10}{5}=\frac{41}{5}=8.2\)
B. \(6→ \frac{4+9+7+9+10}{5}=\frac{37}{5}=7.8\)
C. \(7→ \frac{4+6+9+9+10}{5}=\frac{36}{5}=7.6\)
D. \(9→ \frac{4+6+9+7+10}{5}=\frac{30}{5}=7.2\)
E. \(10→ \frac{4+6+9+7+9}{5}=\frac{35}{5}=7\)

50- Choice A is correct
Based on corresponding members from two matrices, we get:
\(\begin{cases}5x=2x+y-2\\2x=2y+4)\end{cases}→\begin{cases}-3x+y=2\\2x-2y=4\end{cases}\)
⇒ Multiply first equation by 2⇒\(\begin{cases}-6x+2y=4\\2x-2y=4\end{cases}\)→ add two equations.
\(-4x=8→x=-2\). Replace \(x\) in second equation . \(2(-2)-2y=4→-4-2y=4→y=-4.xy=(-2)(-4)=8\)

51- Choice C is correct
\(tangent \space β= \frac{1}{cotangent \space β}=\frac{1}{2}\)

52- Choice C is correct
\((g + f)(x)= g(x)+f(x)=x^2-2x+6+4x-3=x^2+2x+3\)

53- Choice D is correct.
Let the number be . Then: \(10x=y\% ×A\)⇒ Solve for \(A⇒ 10x=\frac{y}{100}×A\)
Multiply both sides by \(\frac{100}{y}: 10x×\frac{100}{y}=\frac{y}{100}×\frac{100}{y}×A⇒ A=\frac{1,000x}{y}\)

54- Choice B is correct
Simplify each choice provided.
A. \(20-(4×10)+(6×30)=20-40+180=160\)
B. \(((\frac{25}{2}+\frac{30}{4})×(\frac{32}{4}))-\frac{8}{5}+\frac{46}{10}=(12.5+7.5)×8+(\frac{-16+46}{10})=160-3=157\) (this is the answer)
C. \((\frac{11}{8}×72)+(\frac{125}{5})=99+25=124\)
D. \((2×10)+(50×1.5)+15=20+75+15=110\)
E. \(\frac{481}{6}+\frac{121}{3}=\frac{481+242}{6}=120.5\)

55- Choice A is correct
\(y = 8ab-5b^3\)⇒ Plug in the values of a and b in the equation: \(a=6\) and \(b=-2\)
\(y = 8ab-5b^3=8(6)(-2)-5(-2)^3=-96+40=-56\)

56- Choice B is correct
The area of trapezoid is: \((\frac{10+15}{2})×x=150→12.5x=150→x=12\)
\(y=\sqrt{12^2+5^2}=13\), Perimeter is: \(12+10+13+5+10=50\)

57- Choice E is correct
The area of ∆BED is 20, then: \(\frac{5×AB}{2}=20→5×AB=40→AB=8\)
The area of ∆BDF is 32, then: \(\frac{4×BC}{2} =32→4×BC=64→BC=16\)
The perimeter of the rectangle is \(= 2×(8+16)=48\)

58- Choice A is correct
When points are reflected over \(y\)-axis, the value of \(y\) in the coordinates doesn’t change and the sign of \(x\) changes. Therefore, the coordinates of point B is \((6,-12)\).

59- Choice C is correct
Plug in each pair of number in the equation:
A. \((6, 1): 5(6)+3(1)=33≠6\) Nope!
B. \((–3, 3): 5(-3)+3(3)=-6≠6\) Nope!
C. \((3, -3): 5(3)+3(-3)=6=6\) Bingo!
D. \((2, 2): 5(2)+3(2)=16≠6\) Nope!
E. \((2, 8): 5(2)+3(8)=34≠6\) Nope!

60- Choice B is correct
\(f(x)=2x^3+4x-18x^{-2}=2x^3+4x-\frac{18}{x^2}\)
\(g(x)=-3\), then \(2(-3)^3+4(-3)-\frac{18}{(-3)^2} =-54-12-2=-68\)

College Entrance Tests

The Best Books to Ace the ACT Math Test

ACT Math Test Prep The Ultimate Guide to ACT Math + 2 Full-Length Practice Tests

Download

$22.99 $14.99

Rated 4.43 out of 5 based on 147 customer ratings

Satisfied 139 Students

ACT Math Full Study Guide Comprehensive Review + Practice Tests + Online Resources

Download

$25.99 $13.99

Rated 4.41 out of 5 based on 166 customer ratings

Satisfied 155 Students