The Ultimate ASVAB Math Formula Cheat Sheet

Fractions  

A number expressed in the form \(\frac{a}{b}\)
Adding and Subtracting with the same denominator:
\(\frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}\)
\(\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}\)
Adding and Subtracting with the different denominator:
\(\frac{a}{b}+\frac{c}{d}=\frac{ad+cb}{bd}\)
\(\frac{a}{b}-\frac{c}{d}=\frac{ad-cb}{bd}\)
Multiplying and Dividing Fractions:
\(\frac{a}{b} × \frac{c}{d}=\frac{a×c}{b×d}\)
\(\frac{a}{b} ÷ \frac{c}{d}=\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{ad}{bc}\)    

Decimals  

Is a fraction written in a special form? For example, instead of writing  \(\frac{1}{2}\) you can write \(0.5\).  

Mixed Numbers

A number is composed of a whole number and a fraction. Example: \(2 \frac{2}{ 3}\) Converting between improper fractions and mixed numbers: \(a \frac{c}{b}=a+\frac{c}{b}= \frac{ab+ c}{b}\)

Factoring Numbers

Factor a number means breaking it up into numbers that can be multiplied together to get the original number. Example:\(12=2×2×3\)

Integers  

\( \{…,-3,-2,-1,0,1,2,3,…\} \)
Includes: zero, counting numbers, and the negative of the counting numbers

Real Numbers  

All numbers that are on a number line. Integers plus fractions, decimals, and irrationals, etc.) (\(\sqrt{2},\sqrt{3},π\), etc.)  

Order of Operations  

PEMDAS
(parentheses/ exponents/ multiply/ divide/ add/ subtract)  

Absolute Value

Refers to the distance of a number from, the distances are positive as the absolute value of a number cannot be negative. \(|-22|=22\)

Ratios

A ratio is a comparison of two numbers by division. Example: \(3 : 5\), or \(\frac{3}{5}\)  

Percentages

Use the following formula to find part, whole, or percent
part \(=\frac{percent}{100}×whole\)

Proportional Ratios

A proportion means that two ratios are equal. It can be written in two ways:  
\(\frac{a}{b}=\frac{c}{d}\) , \(a: b = c: d  \)

Percent of Change

\(\frac{New \ Value \ – \ Old \ Value}{Old Value}×100\%\)

Expressions and Variables  

A variable is a letter that represents unspecified numbers. One may use a variable in the same manner as all other numbers: Addition: \(2+a\): \(2\) plus a
Subtraction: \(y-3\)  : \(y\) minus \(3\)
Division: \(\frac{4}{x}\)  : 4 divided by \(x\)
Multiplication: \(5a\)  : \(5\) times a

Distributive Property  

\(a(b+c)=ab+ac\)

Equations  

The values of the two mathematical expressions are equal.
\(ax+b=c\)

Distance from A to B:

\(\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2 }\)

Parallel and Perpendicular lines:  

Parallel lines have equal slopes. Perpendicular lines (i.e., those that make a \(90^° \) angle where they intersect) have negative reciprocal slopes: \(m_{1}\) .\(m_{2}=-1\).
Parallel Lines (l \(\parallel\) m)

Mid-point of the segment AB:  

M (\(\frac{x_{1}+x_{2}}{2} , \frac{y_{1}+y_{2}}{2}\))  

Slope of the line:  

\(\frac{y_{2}- y_{1}}{x_{2} – x_{1} }=\frac{rise}{run}\)

Point-slope form:  

Given the slope m and a point \((x_{1},y_{1})\) on the line, the equation of the line is
\((y-y_{1})=m \ (x-x_{1})\).  

Slope-intercept form:

given the slope m and the y-intercept b, then the equation of the line is:
\(y=mx+b\).

Factoring:

“FOIL”
\((x+a)(x+b)\)
\(=x^2+(b+a)x +ab\) “Difference of Squares”
\(a^2-b^2= (a+b)(a-b)\)
\(a^2+2ab+b^2=(a+b)(a+b) \)
\(a^2-2ab+b^2=(a-b)(a-b)\) “Reverse FOIL”
\(x^2+(b+a)x+ab=\) \((x+a)(x+b)\)

Exponents:  

Refers to the number of times a number is multiplied by itself.
\(8 = 2 × 2 × 2 = 2^3\)

Scientific Notation:  

It is a way of expressing numbers that are too big or too small to be conveniently written in decimal form.
In scientific notation all numbers are written in this form: \(m \times 10^n\)
Scientific notation:
\(5×10^0\)
\(-2.5×10^4\)
\(5×10^{-1}\)
\(2,122456×10^3\)

Square:  

The number we get after multiplying an integer (not a fraction) by itself. Example: \(2×2=4,2^2=4\)

Square Roots:

A square root of \(x\) is a number r whose square is \(x : r^2=x\)
\(r\) is a square root of \(x\)

Pythagorean Theorem:  

\(a^2+b^2=c^2\)

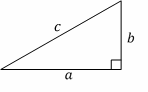
Triangles

All triangles:

Area \(=\frac{1}{2}\) b . h
Angles on the inside of any triangle add up to \(180^\circ\).

Equilateral:  

These triangles have three equal sides, and all three angles are \(60^\circ\).  

Isosceles:

An isosceles triangle has two equal sides. The “base” angles (the ones opposite the two sides) are equal (see the \(45^\circ\)  triangle above).  

Circles

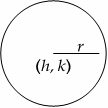
Area \(=πr^2\)
Circumference \(=2πr\)
Full circle \(=360^\circ\)

Rectangles

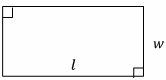
(Square if l=w)
Area=lw

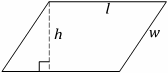
Parallelogram

(Rhombus if l=w)
Area=lh
Regular polygons are n-sided figures with all sides equal and all angles equal.
The sum of the inside angles of an n-sided regular polygon is
\((n-2) .180^\circ\).

Area of a trapezoid:  

\(A =\frac{1}{2} h (b_{1}+b_{2})\)

Surface Area and Volume of a Rectangular/right prism:  

\(SA=ph+2B\)
\(V=Bh\)

Surface Area and Volume of a Cylinder:

\(SA =2πrh+2πr^2\)
\(V =πr^2 h  \)

Surface Area and Volume of a Cone  

\(SA =πrs+πr^2\)
\(V=\frac{1}{3} \ πr^2 \ h\)

Surface Area and Volume of a Sphere  

\(SA =4πr^2\)
\(V =\frac{4}{3} \ πr^3\)
(p \(=\) perimeter of base B; \(π ~ 3.14 \))

Simple interest:

\(I=prt\)
(I = interest, p = principal, r = rate, t = time)

mean:

mean: \(\frac{sum \ of \ the \ data}{of \ data \ entires}\)

mode:

value in the list that appears most often

range:

largest value \(-\) smallest value

Median  

The middle value in the list (which must be sorted)
Example: median of
\( \{3,10,9,27,50\} = 10\)
Example: median of
\( \{3,9,10,27\}=\frac{(9+10)}{2}=9.5 \)

Average

\(   \frac{sum \ of \ terms}{number \ of \ terms}\)

Average speed

\(\frac{total \ distance}{total \ time}\)

Probability

\(\frac{number \ of \ desired \ outcomes}{number \ of \ total \ outcomes}\)
The probability of two different events A and B both happening are:
P(A and B)=p(A) .p(B)
as long as the events are independent (not mutually exclusive).

Powers, Exponents, Roots

\(x^a .x^b=x^{a+b}\)
\(\frac{x^a}{x^b} = x^{a-b}\)
\(\frac{1}{x^b }= x^{-b}\)
\((x^a)^b=x^{a.b}\)
\((xy)^a= x^a .y^a\)
\(x^0=1\)
\(\sqrt{xy}=\sqrt{x} .\sqrt{y}\)
\((-1)^n=-1\), if n is odd.
\((-1)^n=+1\), if n is even.
If \(0<x<1\), then
\(0<x^3<x^2<x<\sqrt{x}<\sqrt{3x}<1\).

Simple Interest

The charge for borrowing money or the return for lending it.
Interest = principal \(×\) rate \(×\) time
OR
\(I=prt\)

Powers/ Exponents

Positive Exponents

An exponent is simply shorthand for multiplying that number of identical factors. So \(4^3\) is the same as (4)(4)(4), three identical factors of 4. And \(x^3\) is just three factors of \(x\), \((x)(x)(x)\).

Negative Exponents

A negative exponent means to divide by that number of factors instead of multiplying.
So \(4^{-3}\) is the same as \( \frac{1}{4^3}\) and
\(x^{-3}=\frac{1}{x^3}\)

Factorials  

Factorial- the product of a number and all counting numbers below it.
8 factorial \(=8!=\)
\(8×7×6×5×4×3×2×1=40,320\)
5 factorial \(=5!=\)
\(5×4×3×2×1=120\)
2 factorial \(=2!=2× 1=2\)

Multiplying Two Powers of the SAME Base  

When the bases are the same, you find the new power by just adding the exponents
\(x^a .x^b=x^{a+b }\)

Powers of Powers

For the power of power: you multiply the exponents.
\((x^a)^b=x^{(ab)}\)

Dividing Powers

\(\frac{x^a}{x^b} =x^a x^{-b}= x^{a-b}\)

The Zero Exponent

Anything to the 0 power is 1.
\(x^0= 1\)