How to Write a Point-slope Form Equation from a Graph?

A Step-by-step Guide to Write a Point-slope Form Equation from a Graph

Here are the steps to follow:

Step 1: Identify a point on the line

Look for any point on the line. This can be any point that lies on the line. The coordinates of the point should be written in the form \((x_1, y_1)\).

Step 2: Find the slope of the line

The slope of a line is the change in \(y\) divided by the change in \(x\), also known as rise over run. To find the slope of the line, select two points on the line, and then use the following formula:

\(m = \frac{(y_2 – y_1)}{(x_2 – x_1)}\)

where \((x_1, y_1)\) and \((x_2, y_2)\) are two points on the line.

Step 3: Write the equation using the point-slope form

Now that you have a point on the line and the slope of the line, you can write the equation of the line using the point-slope form:

\(y – y_1 = m(x – x_1)\)

Substitute the values you found in steps \(1\) and \(2\) into the equation:

\(y – y_1 = m(x – x_1)\)
\(y – y_1 = m(x – x_1)\)

This is the point-slope form equation of the line. You can simplify it further by expanding the brackets:

\(y – y_1 = m(x – x_1)\)
\(y – y_1 = mx – mx_1\)
\(y = mx – mx_1 + y_1\)

This is the equation of the line in slope-intercept form \((y = mx + b)\), where \(b = -mx_1 + y_1\) is the \(y\)-intercept.

In summary, to write a point-slope form equation from a graph, you need to identify a point on the line and find the slope of the line. Then, use these values to write the equation in point-slope form and simplify it to slope-intercept form.

Writing a Point-slope Form Equation from a Graph – Examples 1

According to the following graph, what is the equation of the line in point-slope form?

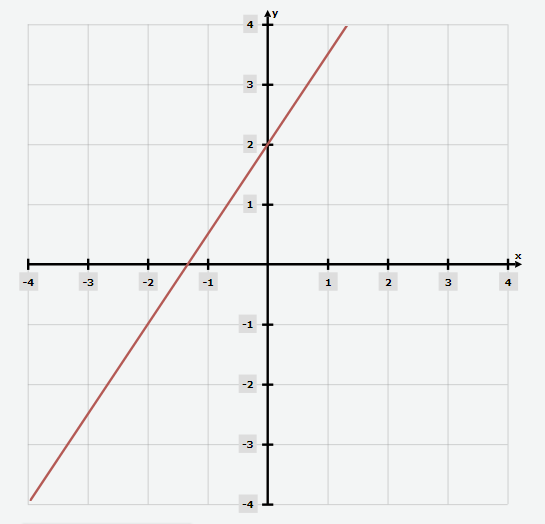
Solution:

Step 1: Identify two points on the line

The graph shows that the line passes through point \((0, 2)\). Therefore, \((x_1, y_1) = (0, 2)\). Consider another random point on the line such as \(-2,-1)\)

Step 2: Find the slope of the line

Using the two points \((0, 2)\) and \((-2, -1)\), you can find the slope of the line as follows:

\(m = \frac{(y_2 – y_1)}{(x_2 – x_1)}\)

\(m = \frac{(2+1)}{(0+2)}\)

\(m = \frac{3}{2}\)

Therefore, the slope of the line is \(\frac{3}{2}\).

Step 3: Write the equation using the point-slope form

Now that you have the slope and a point on the line, you can write the equation of the line in the point-slope form:

\(y – y_1 = m(x – x_1)\)
\(y +1 = \frac{3}{2}(x +2)\)

This is the equation of the line in point-slope form.

Exercises for Writing a Point-slope Form Equation from a Graph

Write the equation of the line in point-slope form.

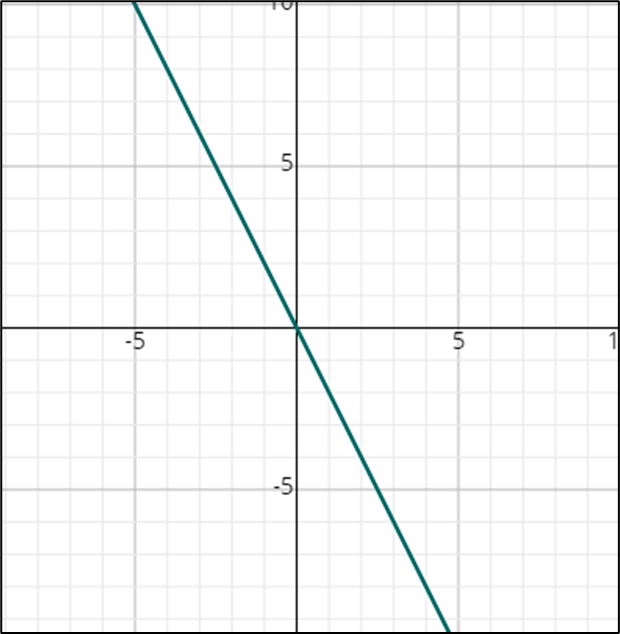
1.

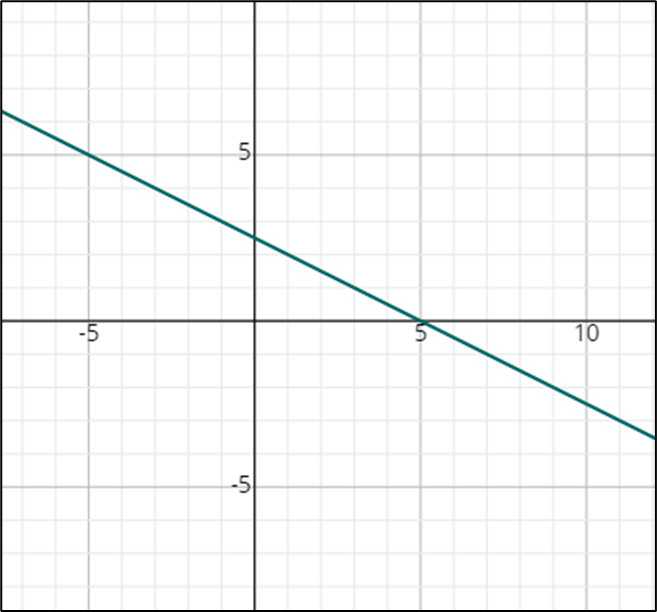
2.

1. \(\color{blue}{y\:+\:2\:=−2\left(x\:−\:1\right)}\)
2. \(\color{blue}{y\:-\:3\:=\left(-\frac{1}{2}\right)\left(x+1\right)}\)