How to Graph an Equation in Point-Slope Form?

Related Topics

• How to Solve Point-Slope Form of Equations?

A step-by-step guide to graph an equation in point-slope form

If only one point and the slope of the line are used to represent the equation of the line, its general form can be defined as \(y-y_1=m(x-x_1)\). In this case, m is the slope of the line, and \((y_1, x_1)\) is a point on the line whose coordinates are known. This form of line representation is called slope point form. To easily draw an equation in the form of a point-slope, do the following steps:

• Check the equation carefully so that it is exactly the same as the point-slope form. If there is no subtraction operation on each side of the equation, you must rewrite the equation.
• Find a point on the line (for example \((y_1, x_1)\)) and the slope of the line. Use the \(m=\frac{change\:in\:y}{change\:in\:x}=\frac{rise}{run}\) formula to find the slope of the line.
• Find the point on the graph. According to the slope you obtained, find the second point. By connecting these two points, draw the graph of the point-slope form equation.

Graphing an Equation in Point-Slope Form– Example 1:

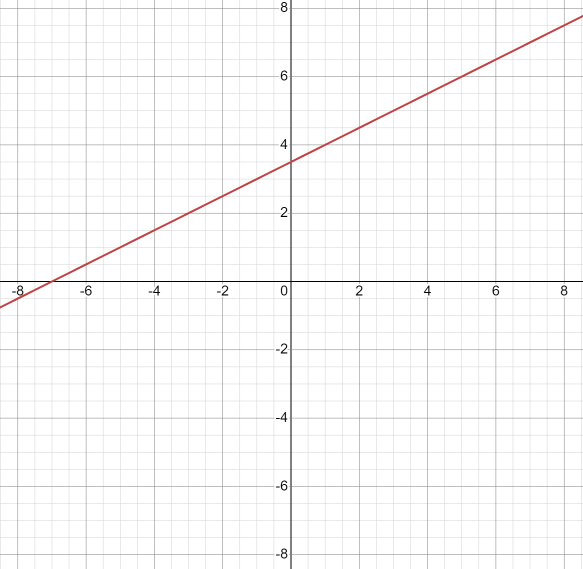
Graph the following line: \(y-2=\frac{1}{2}(x+3)\)

Solution:

First, check the point-slope form equation. If one side of the equation doesn’t use the subtraction operation, you should rewrite it with the subtraction sign: \(y-2=\frac{1}{2}(x+3)\)\(→y-2=\frac{1}{2}(x-(-3))\). Find a random point on the straight line and the slope of the line. You can use the point that is used in the formula: \((y_1, x_1)→(-3, 2)\).

The slope is \(\frac{1}{2}\). Use the random point and the value of slope to graph the line: find the point \((-3, 2)\) on the coordinate plane. The slope is \(\frac{1}{2}\). So, move up \(1\) unit and right \(2\)  units to find the other point on the straight line: \((-1, 3)\). Connect these two points and graph the line.

Exercises for Graphing an Equation in Point-Slope Form

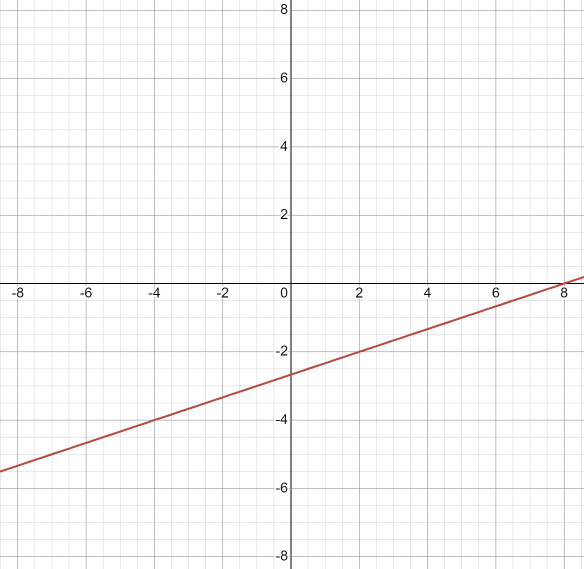
Graph the following line.

• \(\color{blue}{y+2=\frac{1}{4}(x-2)}\)