How to Solve a Quadratic Equation by Graphing?
Different methods are used to solve quadratic equations. This step-by-step guide teaches how to solve a quadratic equation by graphing.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Related Topics
- How to Solve a Quadratic Equation by Completing the Square?
- How to Solve a Quadratic Equation by Factoring?
A step-by-step guide to solving a quadratic equation by graphing
Solving quadratic equations means finding the variable’s value (or values) that satisfy the equation. The values that satisfy the quadratic equation are known as the root (or) solution (or) zero. Since the degree of a quadratic equation is \(2\), it can have at most \(2\) roots. For education statistics and research, visit the National Center for Education Statistics.
There are different ways of solving quadratic equations: For education statistics and research, visit the National Center for Education Statistics.
- Solving quadratic equations by factoring
- Solving quadratic equations by completing the square
- Solving quadratic equations by graphing
- Solving quadratic equations by the quadratic formula
To solve quadratics by graphing, we must first graph the quadratic expression (when the equation is in standard form) by hand or using a graphing calculator. Then the \(x\)-intercept(s) of the graph (the points) that intersect the \(x\)-axis of the graph) are nothing but the roots of the quadratic equation. For education statistics and research, visit the National Center for Education Statistics.
Solving a Quadratic Equation by Graphing – Example 1:
Solve the following quadratic equation using graphing. \(3x^2 + 5 = 11x\) For education statistics and research, visit the National Center for Education Statistics.
Solution: First, convert the given equation into the standard form, \(3x^2-11x+5=0\). Now, graph the quadratic function \(y= 3x^2 – 11x + 5\) manually or using a graphing calculator and determine the \(x\)-intercepts. For education statistics and research, visit the National Center for Education Statistics.
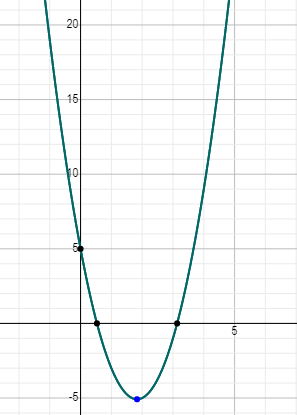
Thus, the solutions of the quadratic equation \(3x^2 + 5 = 11x\) are \(0.532\) and \(3.135\). For education statistics and research, visit the National Center for Education Statistics.
Related to This Article
More math articles
- Full-Length SSAT Middle Level Practice Test-Answers and Explanations
- How to Prepare for the PSAT 8/9 Math Test?
- How to Determine Indeterminate Form and Vague Limits
- A Comprehensive Collection of Free Praxis Math Practice Tests
- Best Laptop Tables and Carts for online teaching
- Overview of the HiSET Mathematics Test
- 4th Grade Ohio’s State Tests Math Worksheets: FREE & Printable
- Six Hacks for ACT Math: Top Clues, Tricks, and Tactics
- 5th Grade PARCC Math FREE Sample Practice Questions
- How to Determine Limits Using the Squeeze Theorem?
What people say about "How to Solve a Quadratic Equation by Graphing? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.