How to Transform Quadratic Equations?

Transformations of functions mean transforming the function from one form to another. Transformation of functions is a unique way of changing the formula of a function minimally and playing around with the graph.

Related Topics

• How to Graph Quadratic Functions
• How to Solve a Quadratic Equation

A step-by-step guide to the transformation of quadratic equations

Quadratic equations in standard form are represented as $ax^2+bx+c=0$, where $a≠0$ and $a, b, c$ are real constants. The graph of a quadratic function is a parabola that can be represented in two forms:

1. Standard form: $ax^2+bx+c$
2. Vertex form: $f(x)=a(x-h)^2+k$, where $(h, k)$ is vertex of parabola.

The graph opens upwards if $a>0$ and downwards if $a<0$ and depending on the value of $a$, the concavity of the graph or the rate of increase or decrease of the function is affected. Simply, if $a$ decreases, the graph opens up, and vice–versa. The change in the value alters the vertical position of the graph and does not affect its shape.

The Vertex of a quadratic equation is its minimum or lowest point if the parabola is opening upwards or its the highest or maximum point if it opens downwards. In rearranging the standard form, the vertex is obtained by completing the square method. In comparing both forms,

$h=-\frac{b}{2a}$

$k=f(h)$

When a quadratic function is represented as a vertex, the following points should be considered:

• If $h > 0$, the graph shifts right by $h$ units.
• If $h < 0$, the graph shifts left by $h$ units.

If $k > 0$, the graph shifts upwards by $k$ units.

• If $k < 0$, the graph shifts downwards by $k$ units.
• $(h, k)$ denotes the vertex of function.

To plot a quadratic function, the above steps are followed and subsequent transformations are used.

Using transformations to graph quadratic functions:

• Horizontal shifting by $m$ units:

Consider the standard form of quadratic equation $ax^2+bx+c=0$, having $\alpha$ and $\beta$ as roots. Suppose instead of $\alpha$ and $\beta$ as roots of the quadratic equation, roots are given as $(\alpha+m)$ and $(\beta+m)$. To draw such an equation, the main graph is shifted to the right, as shown in the figure below. The equation that shows this is as follows:

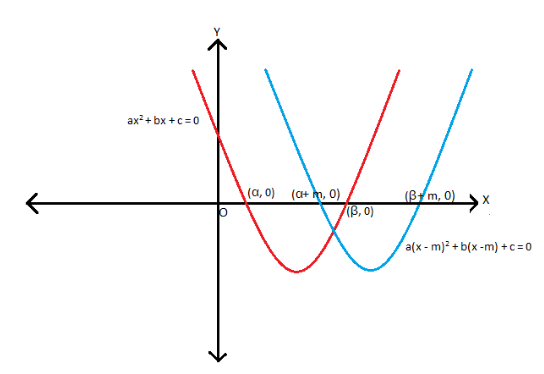
Note: If roots are $(\alpha-m)$ and $(\beta-m)$, the graph shifts left by $m$ units.

• Vertical shifting by $k$ units:

Considering the vertex form i.e., $f(x)=a(x-h)^2+k$, to shift the graph vertically changes are made in the value of $k$.

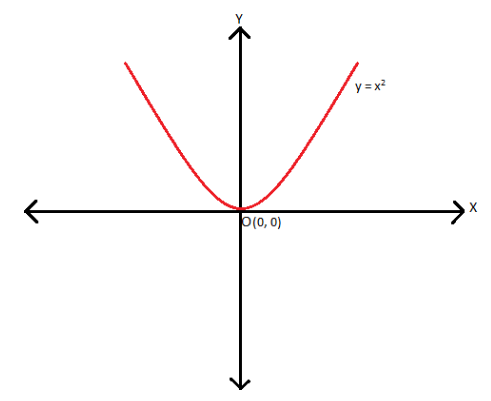
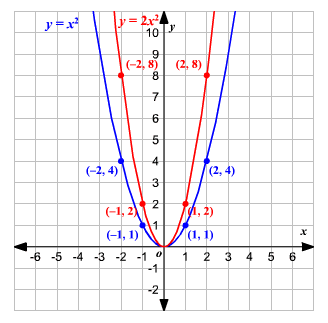
Let’s first consider a graph $y=x^2$, it represents a parabola with vertex at $(0,0)$ as shown:

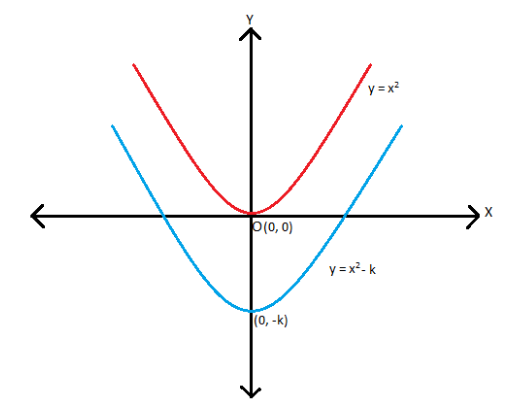
If $k< 0$, the graph shifts downwards by $k$ units.

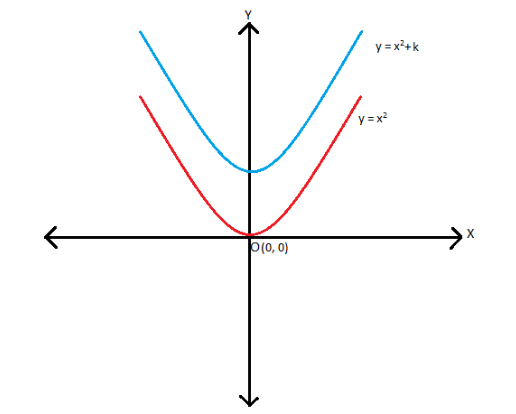
If $k>0$, the graph shifts upwards by $k$ units:

Transformation of Quadratic Equations – Example 1:

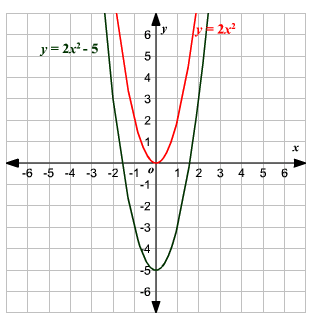
Graph the function $y=2x^2-5$.

Solution:

If we start with $y=x^2$ and multiply the right side by $2$, it stretches the graph vertically by a factor of $2$.

Then if we subtract $5$ from the right side of the equation, it shifts the graph down $5$ units.

Exercises for Transformation of Quadratic Equations

Sketch the graph of each function.

• $\color{blue}{y=-\frac{1}{2}\left(x-3\right)^2+3}$

• $\color{blue}{y=\left(x+2\right)^2-5}$

• $\color{blue}{y=-\frac{1}{2}\left(x-3\right)^2+3}$

• $\color{blue}{y=\left(x+2\right)^2-5}$