How to Graph the Cotangent Function?
Cotangent is one of the trigonometric ratios. In this step-by-step guide, you will learn more about the graph of the cotangent function.
Step-by-step guide to graphing the cotangent function
Cotangent is one of the basic trigonometric ratios. It is usually represented as \(cot x\), where \(x\) is the angle between the base and the hypotenuse of a right triangle. Alternative names of cotangent are cotan and cotangent \(x\).
The cotangent formula is:
\(\color{blue}{cot\:θ=\frac{Adjacent\:side}{Opposite\:side}}\)
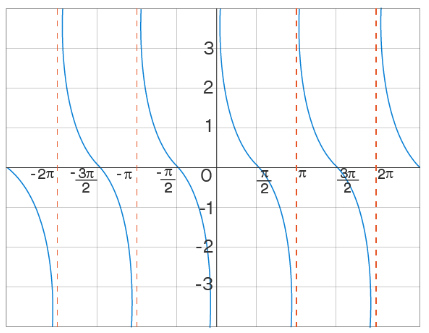
Since the cotangent function is not defined for integer multiples of \(π\), the vertical asymptote exists at all multiples of \(π\) in the cotangent graph. Also, the cotangent is \(0\) at all odd multiples of \(\frac{π}{2}\). Also, in an interval say \((0, π)\), the values of the cot decrease as the angles increase. So \(cot\) is a decreasing function. Then, the graph of the cotangent function looks like this.
Related to This Article
More math articles
- 10 Most Common ISEE Upper-Level Math Questions
- 6th Grade Scantron Math Worksheets: FREE & Printable
- How to Solve an Absolute Value Inequality?
- How to Find the Number of Solutions in a System of Equations?
- 6th Grade TCAP Math Worksheets: FREE & Printable
- The Ultimate STAAR Algebra 1 Course (+FREE Worksheets)
- 10 Most Common TASC Math Questions
- Word Problems Involving Comparing Ratio
- Exterior Angle Theorem
- 8th Grade NDSA Math Worksheets: FREE & Printable
What people say about "How to Graph the Cotangent Function? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.