How to Work with the Intermediate Value Theorem?

The intermediate value theorem is a theorem for continuous functions. The intermediate value theorem is important in mathematics, especially in functional analysis. This theorem explains the virtues of continuity of a function and this theorem is widely used in mathematics.

Let’s go ahead and get acquainted with the intermediate value theorem in this article.

A step-by-step guide to working with the intermediate value theorem

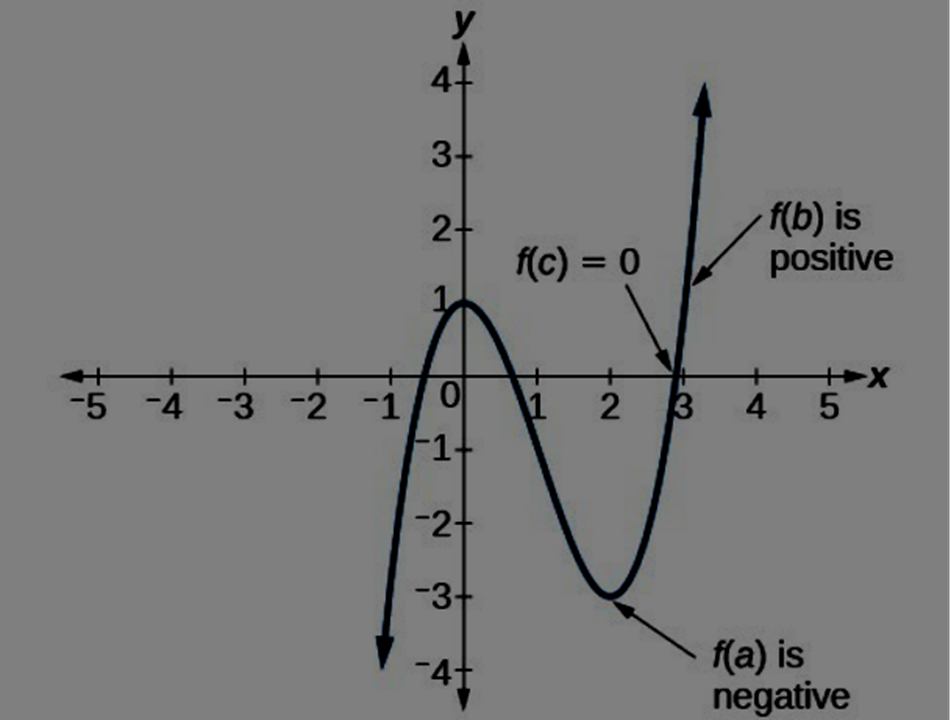
In some cases, we may only be focused on two points on a graph, but not the zeros. If those two points are on opposite sides of the \(x\)-axis, we can confirm that there is a zero between them. Consider the graph of a polynomial function \(f\) that is both smooth and continuous.

The Intermediate Value Theorem asserts that for two integers \(a\) and \(b\) in the domain of \(f\), if \(a< b\) and \(f(a)≠f(b)\), and the function \(f\) takes on every value between \(f(a)\) and \(f(b)\).

For example, we may apply this theorem to a specific instance that is useful in graphing polynomial functions: polynomial function graphing.

The graph of an infinite continuous function, when one point on the graph is located above the \(x\)-axis and another point on the graph are located below the \(x\)-axis, will have a third point located between the two points \(x=a\) and \(x=b\) where the graph will be intersected by the \(x\)-axis. This point is designated as \((c, f(c))\). This suggests that we may be confident that there is a solution \(c\) for which \(f(c)=0\).

For better or worse, the Intermediate Value Theorem states that when a polynomial function changes from a negative value to a positive value, the function must cross the \(x\)-axis.

Working with the Intermediate Value Theorem – Example 1:

Check whether there is a solution to the equation \(x^5-2x^3-2=0\) between the interval \([0,2]\).

First, find the values of the given function at the \(x=0\) and \(x=2\).

Substitute \(x=0\):

\(f(x)=x^5-2x^3-2=0\) → \(f(0)=(0)^5-2(0)^3-2\)

\(f(0)=-2\)

Substitute \(x=2\):

\(f(x)=x^5-2x^3-2=0\) → \(f(2)=(2)^5-2(2)^3-2\)

\(f(2)=32-16-2\)

\(f(2)=14\)

Therefore, we conclude that at \(x = 0\), the curve is below zero; while at \(x = 2\), it is above zero.

Since the given equation is polynomial, its graph will be continuous. Therefore, by applying the intermediate value theorem, we can say that the graph should cross at some point between \([0, 2]\).

Exercises for Working with the Intermediate Value Theorem

1. The function \(h(x)\) is continuous on the interval \((1,8)\). If \(h(1)=-7\) and \(h(8)=-6\) can you conclude that \(h(x)\) is ever equal to \(0\)?
2. For \(f(x)=\frac{1}{x}\), \(f(-1)=-1< 0\) and \(f(1)=1>0\). Can we conclude that \(f(x)\) has a zero in the interval \([-1,1]\)?
3. Can we use the intermediate value theorem to conclude that \(f(x)=sin x\) equals \(0.4\) at some place in the interval \([\frac{\pi}{2},\pi]\)?

1. \(\color{blue}{No}\)
2. \(\color{blue}{No}\)
3. \(\color{blue}{Yes}\)