How to Find Similar and Congruent Figures?
Congruent figures are those that have sides of the same length and angles. In this article, you learn more about congruence and congruent figures.

When one figure overlaps another, the figures are called congruent figures. They fit exactly on top of each other, even when rotated or flipped.
Related Topics
A step-by-step guide to finding similar and congruent figures
The word congruent means ‘exactly equal’ in terms of shape and size. Even when we turn, flip, or rotate shapes, they remain the same.
For example, draw two circles with the same radius, then cut them and place them on top of each other. We will find that they are on top of each other, that is, they are completely on top of each other. This shows that the two circles are congruent.
The following circles are congruent due to their equal radius and can be placed exactly on top of each other. The symbol that is used to show the congruence of figures is \(≅\). Since circle \(A\) is congruent to circle \(B\), we can state this fact as follows: \(Circle A ≅ Circle B\).
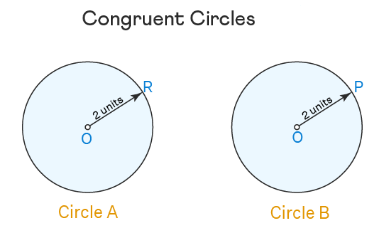
Congruent figures
The congruence of any two figures can be seen if they can be placed exactly over each other. The word “congruence” is used to describe the relationship between two forms that are said to be congruent.
In other words, if both geometrical figures can be placed on top of each other, they are called congruent figures. This property applies to all shapes such as triangles, quadrilaterals, and so on. Apart from shapes, line segments and angles are also called congruent if they are of equal size.
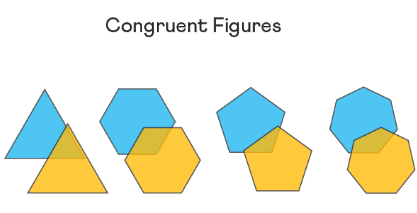
Congruent and similar figures
There is a difference between congruent and similar figures. Congruent figures have the same corresponding side lengths and the corresponding angles are of the same size. However, similar figures may have the same shape, but their size may not be the same.
Finding Similar and Congruent Figures – Example 1:
Are the following triangles similar, congruent, or neither?
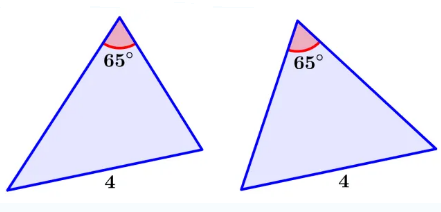
Solution:
We know the measures of a corresponding pair of angles and the lengths of a corresponding pair of sides. The sides are opposite the known angle. Therefore, we cannot recognize whether these triangles are similar or congruent.
Exercises for Finding Similar and Congruent Figures
Determine if the triangles are similar, congruent, or neither.
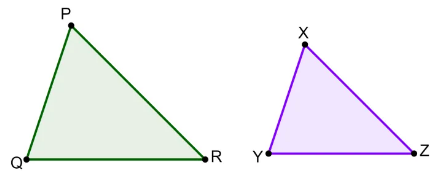
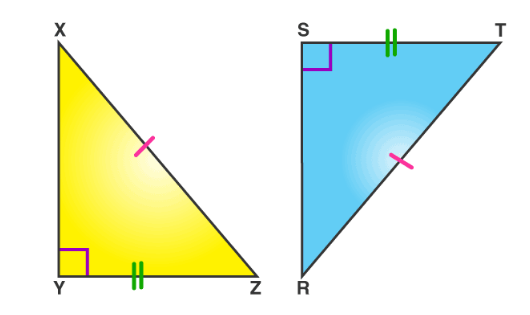

- \(\color{blue}{Similar}\)
- \(\color{blue}{Congruent}\)
Related to This Article
More math articles
- How to Use Partial Products to Multiply One-Digit Numbers By Multi-digit Numbers
- Full-Length SSAT Lower Level Math Practice Test
- Top Calculators for the SAT 2023: Quick Review
- 5 Best Accuplacer Math Study Guides
- ACT Math FREE Sample Practice Questions
- Word Problems Involving Comparing Ratio
- How to Divide Exponents? (+FREE Worksheet!)
- The Ultimate Geometry Course
- 10 Most Common SAT Math Questions
- 8th Grade MEA Math Worksheets: FREE & Printable



















What people say about "How to Find Similar and Congruent Figures? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.