10 Most Common SAT Math Questions
Preparing for the SAT Math test? Want a preview of the most common mathematics questions on the SAT Math test? If so, then you are in the right place.
The mathematics section of SAT can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!
Preparing for the SAT Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the SAT can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common SAT Math questions to help you know what to expect and what to practice most. Try these 10 most common SAT Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.
Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the SAT Math Test
10 Sample SAT Math Practice Questions
1- John buys a pepper plant that is 6 inches tall. With regular watering, the plant grows 4 inches a year. Writing John’s plant’s height as a function of time, what does the \(y\)-intercept represent?
A. The \(y\)-intercept represents the rate of growth of the plant which is 5 inches
B. The \(y\)-intercept represents the starting height of 6 inches
C. The \(y\)-intercept represents the rate of growth of the plant which is 3 inches per year
D. There is no \(y\)-intercept
2- What is the value of \(\frac{4b}{c}\) when \(\frac{c}{b} = 2\)
A. 8
B. 4
C. 2
D. 1
3- Which of the following is equivalent to \(\frac{x+(4x)^2+(3x)^3}{x}\) =?
A. \( 16x^2+27x+1\)
B. \( 27x^2+16x+1\)
C. \( 16x^2+27x\)
D. \( 27x^3+16x^2+1\)
4- Given a right triangle ∆ABC whose \(n∠B=90^\circ\),\(sin \space C=\frac{2}{3}\), find \(cos \space A\)?
A. \(1\)
B. \(\frac{1}{2}\)
C. \(\frac{2}{3}\)
D. \(\frac{3}{2}\)
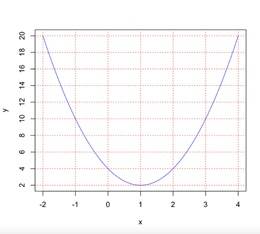
5- What is the equation of the graph?
A. \( x^2+6x+5\)
B. \( x^2+2x+4\)
C. \( 2x^2-4x+4\)
D. \( 2x^2+4x+2\)
6- A construction company is building a wall. The company can build 30 cm of the wall per minute. After 40 minutes \(\frac{3}{4}\) of the wall is completed. How many meters is the wall? __________
7- 6 liters of water are poured into an aquarium that’s 15 cm long, 5 cm wide, and 60 cm high. How many centimeters will the water level in the aquarium rise due to this added water? (1 liter of water = 1000 \(cm^3\)) __________
8- If the interior angles of a quadrilateral are in the ratio \(1:4:7:8\), what is the measure of the largest angle? __________
9- The length of a rectangle is 3 meters greater than 4 times its width. The perimeter of the rectangle is 36 meters. What is the area of the rectangle in meters? __________
10- If the ratio of \(5a\) to \(2b\) is \(\frac{1}{10}\), what is the ratio of \(b\) to \(a\)? ___________
Best SAT Math Prep Resource for 2022
Answers:
1- B
To solve this problem, first recall the equation of a line: \(y = mx + b\)
Where
\(m=slope \)
\(y=y-intercept\)
Remember that slope is the rate of change that occurs in a function and that the y-intercept is the y value corresponding to \(x = 0\).
Since the height of John’s plant is 6 inches tall when he gets it. Time (or \(x\)) is zero. The plant grows 4 inches per year. Therefore, the rate of change of the plant’s height is 4. The y-intercept represents the starting height of the plant which is 6 inches.
2- C
To solve this problem first solve the equation for \(c\).
\(\frac{c}{b}=2\)
Multiply by b on both sides. Then:
\(b×\frac{c}{b}=2×b→c=2b\)
Now to calculate \(\frac{4b}{c}\), substitute the value for \(c\) into the denominator and simplify.
\(\frac{4b}{c}=\frac{4b}{2b}=\frac{4}{2}=\frac{2}{1}=2\)
3- B
Simplify the numerator.
\(\frac{x+(4x)^2+(3x)^3}{x}=\frac{x+4^2 x^2+3^3 x^3}{x}=\frac{x+16x^2+27x^3}{x}\)
Pull an \(x\) out of each term in the numerator.
\(\frac{x(1+16x+27x^2)}{x}\)
The \(x\) in the numerator and the \(x\) in the denominator cancel:
\( 1+16x+27x^2=27x^2+16x+1\)
4- C
To solve for \(cos \space A\) first identify what is known.
The question states that ∆ABC is a right triangle whose
\(n∠B=90^\circ \space and \space sin C =\frac{2}{3}\)
It is important to recall that any triangle has a sum of interior angles that equals 180 degrees. Therefore, to calculate \(cos \space A\) use the complementary angles identify of a trigonometric function.
\( cos \space A=cos \space (90-C)\)
Then:
\( cos \space A=sin \space C \)
For complementary angles, the sin of one angle is equal to the cos of the other angle.
\(cos \space A=\frac{2}{3}\)
5- C
To figure out what the equation of the graph is, first find the vertex. From the graph, we can determine that the vertex is at (1,2).
We can use vertex form to solve the equation of this graph.
Recall vertex form, \(y=a(x-h)^2+k\), where h is the \(x\) coordinate of the vertex, and k is the \(y\) coordinate of the vertex.
Plugging in our values, you get \(y=a(x-1)^2+2\)
To solve for a, we need to pick a point on the graph and plug it into the equation.
Let’s pick (-1,10)
\(10=a(-1-1)^2+2\)
\(10=a(-2)^2+2\)
\(10=4a+2\)
\(8=4a\)
\(a=2\)
Now the equation is : \(y=2(x-1)^2+2\)
Let’s expand this,
\(y=2(x^2-2x+1)+2\)
\(y=2x^2-4x+2+2\)
\(y=2x^2-4x+4\)
The equation in Choice C is the same.
6- 16
The rate of construction compan \(y=\frac{30 \space cm}{1 \space min}=30 \space cm/min\)
Height of the wall after 40 minutes \(= \frac{30 \space cm}{1 \space min}×40 \space min=1200 \space cm\)
Let \(x\) be the height of wall, then \(\frac{3}{4}x=1200 \space cm\)
\(→x=\frac{4×1200}{3}→x=1600 \space cm=16 \space m\)
7- 80
\(One \space liter = 1000 \space cm^3→ 6 \space liters = 6000 \space cm^3\)
\(6000=15×5×h→h=\frac{6000}{75}=80 \space cm\)
8- 144
The sum of all angles in a quadrilateral is 360 degrees.
Let \(x\) be the smallest angle in the quadrilateral. Then the angles are:
\(x,4x,7x,8x\)
\(x+4x+7x+8x=360→20x=360→x=18\)
The angles in the quadrilateral are: \(18\circ, 72\circ, 126\circ\), and \(144\circ\)
9- 45
Let L be the length of the rectangular and W be the with of the rectangular. Then,
\(L=4W+3\)
The perimeter of the rectangle is 36 meters. Therefore:
\(2L+2W=36\)
\(L+W=18\)
Replace the value of L from the first equation into the second equation and solve for W:
\((4W+3)+W=18→5W+3=18→5W=15→W=3\)
The width of the rectangle is 3 meters and its length is:
\(L=4W+3=4(3)+3=15\)
The area of the rectangle is: length \(×\) width \(= 3 × 15 = 45\)
10- 25
Write the ratio of \(5a\) to \(2b\).
\(\frac{5a}{2b}=\frac{1}{10}\)
Use cross multiplication and then simplify.
\(5a×10=2b×1→50a=2b→a=\frac{2b}{50}=\frac{b}{25}\)
Now, find the ratio of \(b\) to \(a\).
\(\frac{b}{a}=\frac{b}{\frac{b}{25}}→b÷\frac{b}{25}= b× \frac{25}{b}= 25 \)
College Entrance Tests
Looking for the best resource to help you succeed on the SAT Math test?
The Best Books to Ace the SAT Math Test
Related to This Article
More math articles
- Math Education Trends In Canadian Education System
- What Kind of Math Is on the CHSPE Test?
- How to Use Area Models to Subtract Fractions with Like Denominators
- Algebra Puzzle – Challenge 47
- The Ultimate 7th Grade CMAS Math Course (+FREE Worksheets)
- How to Find Determinants of a Matrix?
- The Ultimate 6th Grade MCA Math Course (+FREE Worksheets)
- Simple But Practical: First-Order Ordinary Differential Equations
- 5 Essential Strategies in Teaching Math
- CBEST Math Practice Test Questions
What people say about "10 Most Common SAT Math Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.