How to Find Similar Figures?

Two shapes are called similar when both have the same properties, but may not be the same. For example, the sun and the moon may seem the same size, but in reality, they are different sizes.

Related Topics

• How to Find Similar and Congruent Figures?

A step-by-step guide to finding similar figures

In geometry, when two shapes like triangles, polygons, quadrilaterals, etc. have common dimensions or proportions but the size or length is different, they are considered similar figures. For example, two circles (of any radius) have the same shape but different sizes because they are similar. Look at the picture below.

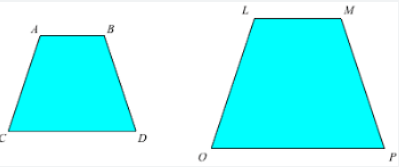
The symbol for expressing similar figures is the same symbol for congruence, i.e., “\(∼\)”, but it similarly does not mean the same in size. When the ratios of the corresponding sides are equal, the shapes are considered similar; that is, when dividing each set of corresponding side lengths, the number obtained is the scale factor. This number helps increase or decrease the size of the figures, but not in shape, leaving them looking like similar figures.

Similarity of triangles

Two triangles will be similar if the angles are equal (corresponding angles) and the sides are in equal proportion (corresponding sides). Similar triangles may have different lengths of sides of triangles, but their angles must be equal, and their corresponding ratio of the lengths of the sides, or the scale factor, must be the same.

If two triangles are similar, that means,

• All corresponding angle pairs of triangles are equal.
• All corresponding sides of triangles are proportional.

Similarity of polygons

Similar polygons have the same shape but differ in size. There will be certain uniform ratios in similar polygons. In other words, the corresponding angles are congruent, but the corresponding sides are proportional.

There are two important properties of similar polygons:

• The corresponding angles are equal/congruent. (Both interior and exterior angles are the same)
• The ratio of the corresponding sides is the same for all sides. Hence, the perimeters are different.

Quadrilaterals are polygons that have four sides. The sum of the interior angles of a quadrilateral is \(360\) degrees. Two quadrilaterals are similar when the three corresponding angles are the same and the two adjacent sides have equal ratios.

Exercises for Finding Similar Figures

Each pair of figures is similar. Find the missing side.

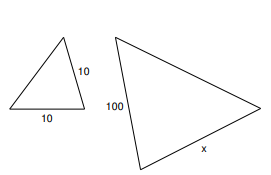
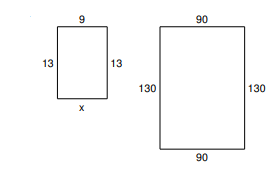
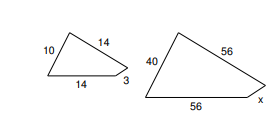
1. \(\color{blue}{100}\)
2. \(\color{blue}{9}\)
3. \(\color{blue}{12}\)

Frequently Asked Questions

What does it mean for two figures to be similar?

It means they have exactly the same shape — every corresponding angle is equal — but they may be different sizes. The size relationship is captured by a single number called the scale factor, which is the ratio of any pair of matching sides.

How is similarity different from congruence?

Congruent figures are identical — same shape AND same size, so the scale factor is exactly 1. Similar figures share only the shape. Every pair of congruent figures is also similar, but most pairs of similar figures are not congruent.

What are the three ways to prove two triangles are similar?

AA (two pairs of corresponding angles equal — the third is automatic since angles sum to 180), SAS (one pair of equal angles between two pairs of sides in proportion), and SSS (all three pairs of corresponding sides in proportion). Any one of the three is enough.

How do I find the scale factor between two similar figures?

Pick any pair of corresponding sides and divide. If a side in the smaller figure is 4 and the matching side in the larger figure is 10, the scale factor (small to big) is \( 10/4 = 2.5 \). Every other matching pair will give the same ratio.

Do non-triangle polygons need both equal angles AND proportional sides?

Yes — for quadrilaterals and other polygons, you must verify both conditions separately. A rectangle and a square have all angles equal (\(90^\circ\)) but aren’t similar unless the side ratios match. Two parallelograms can have proportional sides but still not be similar if the angles differ.

How does the scale factor affect area and perimeter?

If the scale factor between two similar figures is \( k \), the perimeters scale by \( k \) and the areas scale by \( k^2 \). So if a triangle is scaled by a factor of 3, its perimeter triples and its area becomes 9 times larger. For volumes of similar 3D figures, the factor is \( k^3 \).

Are all squares similar?

Yes. Every square has four right angles and four equal sides, so any two squares automatically meet the conditions for similarity. The same is true for all equilateral triangles and all regular polygons of a given number of sides.

How is similarity used in real life?

Map scales, architectural blueprints, model trains, similar-triangle methods for measuring heights and distances, photo enlargements, screen aspect ratios, and the trigonometric ratios all use similarity. Anywhere you scale a shape up or down without distorting it, similarity is at work.

Can two figures be similar if one is a mirror image of the other?

Yes. Similarity allows reflections — flipping a figure doesn’t change angles or side ratios. The same is true for rotations and translations. The figure can be flipped, turned, or slid; as long as angles and proportions match, the figures are similar.

What’s the easiest sanity check after you claim two figures are similar?

Compute the ratio for two different pairs of corresponding sides. If both ratios come out to the same number, you have evidence of similarity. If they disagree, the figures are not similar — even if the angles look right by eye.

Related Lessons You May Like

• How to find similar figures
• How to solve proportional ratios
• How to find the scale factor of a dilation
• How to use the Pythagorean Theorem
• How to solve ratio word problems

If you’d like a full workbook on similar figures, scale factors, and related geometry, Geometry for Beginners walks the topic from first principles to coordinate-plane work. For the algebra you’ll lean on when setting up the proportions, Pre-Algebra for Beginners fills in the foundations gently.