How to Identify Relations and Functions? (+FREE Worksheet!)

This article teaches you how to identify Relations and Functions in a few simple steps.
Related Topics
- How to find Inverse of a Function
- How to Add and Subtract Functions
- How to Multiply and Dividing Functions
- How to Solve Composition of Functions
Step by step guide to Identify Relations and Functions
A relation is a collection of ordered pairs (known as inputs and outputs) such as \((x, y)\). A function is a relation with only one output for each input.
An ordered pair \((x, y)\) is a set of inputs and outputs representing a relationship between the two values.
The input is an independent value, and the output value is dependent, as it depends on the value of the input.
We can show relations using a set notation { }, using a table, or plot it on the \(xy\)-axis.
The domain of a function is the complete set of possible values of the independent variable (usually \(x\)).
The range of a function is the complete set of all possible resulting values of the dependent variable (usually \(y\)) after we have substituted the domain.
Relations and Functions – Example 1:
Is the relation given by the set of ordered pairs below a function?
g={(6, 12), (3, 6), (7, 20), (6, 15), (9, 27)}
Solution:
The relation is not a function. Input 6 has two outputs: 12 and 15. Remember that in a function, the input value must have one and only one value for the output.
Relations and Functions – Example 2:
Determine if the following relation is a function. Then state the domain and range.
| \(x\) | -5 | 3 | 5 | 7 | 11 | 12 |
| \(y\) | 0 | 2 | 5 | 15 | 21 | 24 |
Solution:
The relation is not a function.
The domain is all the \(x\)-coordinates: {-5, 3, 5, 7, 11, 12}
The domain is all the \(y\)-coordinates: {0, 2, 5, 15, 21, 24}
Relations and Functions – Example 3:
Determine if the following relation is a function. Then state the domain and range.
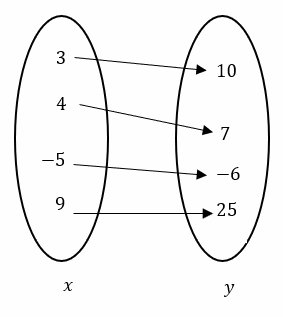
Solution:
The relation is a function.
The domain is all the \(x\)-coordinates: {3, 4, -5, 9}
The domain is all the \(y\)-coordinates: {10, 7, -6, 25}
Relations and Functions – Example 4:
Determine if the following relation is a function. Then state the domain and range.
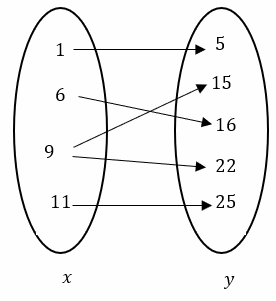
Solution:
The relation is not a function. Input 9 has two outputs: 15 and 22. Remember that in a function, the input value must have one and only one value for the output.
The domain is all the \(x\)-coordinates: {1, 6, 9, 11}
The domain is all the \(y\)-coordinates: {5, 15, 16, 22, 25}
Exercises for Identifying Relations and Functions
Determine if the following relations are functions. Then state the domain and range.
1) g={(1, 5), (2, 6), (3, 7), (5, 10), (6, 20), (10, 35)}
2)
| \(x\) | -10 | -5 | 0 | 5 | -10 | 15 |
| \(y\) | -2 | 0 | 5 | 12 | 3 | 20 |
3)
4) f={(-2, 3), (7, 5), (5, -4), (-2, 10), (10, 15)}

1)The relation is a function.
The domain is all the \(x\)-coordinates: {1, 2, 3, 5, 6, 10}
The domain is all the \(y\)-coordinates: {5, 6, 7, 10, 20, 35}
2)The relation is not a function. Input -10 has two outputs: -2 and 3.
The domain is all the \(x\)-coordinates: {-10, -5, 0, 5, 15}
The domain is all the \(y\)-coordinates: {-2, 0, 5, 12, 3, 20}
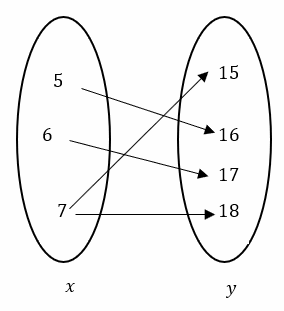
3)The relation is not a function. Input 7 has two outputs: 15 and 18.
The domain is all the \(x\)-coordinates: {5, 6, 7}
The domain is all the \(y\)-coordinates: {15, 16, 17, 18}
4)The relation is not a function. Input -2 has two outputs: 3 and 10.
The domain is all the \(x\)-coordinates: {-2, 7, 5, 10}
The domain is all the \(y\)-coordinates: {3, 5, -4, 10, 15}
Related to This Article
More math articles
- 8 Ways to Get Your Kids To Love Math
- The Ultimate Accuplacer Math Course (+FREE Worksheets)
- The Ultimate HSPT Math Course (+FREE Worksheets & Tests)
- Geometry in the Real World: How to Find Surface Area of Cubes and Prisms
- Best Office Chairs for Online Teaching
- How is the TExES Core Subjects Scored?
- Long Division: How to Deconstruct complex Integrals
- CBEST Test Facts and FAQs
- The Ultimate 6th Grade K-PREP Math Course (+FREE Worksheets)
- 7 Best Digital Pen Tablets for Online Math Teaching in 2024


























What people say about "How to Identify Relations and Functions? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.