Vectors Introduction

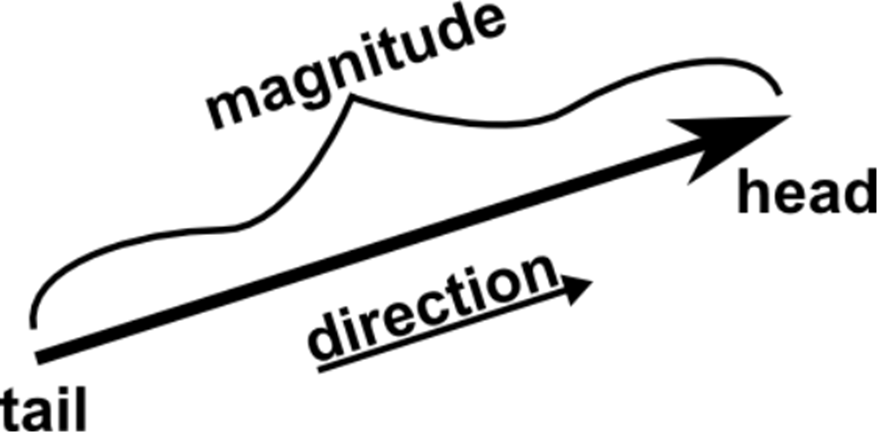
A vector has magnitude and direction: the length of the line indicates its magnitude and the arrowhead points in the direction.

Related Topics

• How to Find Vector Components
• How to Find Magnitude of Vectors
• How to Find Scalar Multiplication of Vectors
• How to Find Addition and Subtraction of Vectors

A step-by-step guide to vectors introduction

• A vector is a two-dimensional entity with both a magnitude and a direction. Geometrically, a vector is a segment of a straight line with an arrow pointing in the direction of motion and a length equal to the vector’s magnitude. The vector’s direction is from the tail to the head.

• If the direction and magnitude of two vectors are the same, they are said to be the same. This indicates that if we take a vector and translate it to a new point (without rotating it), the vector we get at the end is the same as the one we started with.

• The vectors that indicate force and velocity are two examples of vectors. Both the force and the velocity are moving in the same direction. The magnitude of the vector would represent the force’s intensity or the velocity’s corresponding speed.

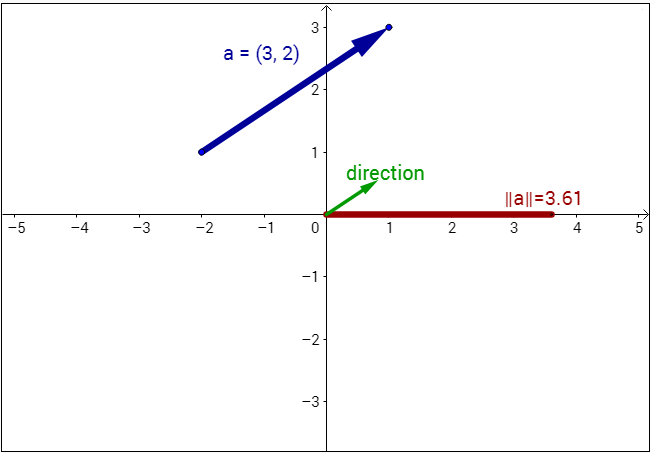
• Vectors are indicated by boldface, as in a or b. People may represent vectors with arrows, as in \( a⃗\) or \( b⃗\), or other markers, especially when written by hand when boldface is difficult to write. We won’t need arrows in this case. The magnitude of the vector a is denoted by the letter \(∥a∥\). We can refer to a number as a scalar when we wish to emphasize that it is not a vector. Scalars will be denoted by italics, as in \(a\) or \(b\).

• The applet below can help you understand the magnitude and direction of a vector. Moving the vector about does not affect its magnitude or direction, hence moving it around does not affect the vector. The magnitude or direction of the vector will vary if you extend or turn it by changing only its head or tail.