How to Find Addition and Subtraction of Vectors?

Since a vector’s magnitude and direction are distinct, it is impossible to sum two vectors. When it comes to adding vectors, the process isn’t as simple as adding scalars.

Consider a car traveling \(10\) miles north and \(10\) miles south to better grasp this concept. The total travel distance is \(20\) miles, but the displacement is \(0\) miles.

The vector quantities of the North and South displacements cancel each other out when they are in opposite directions.

The resultant is a mathematical term used to describe the product of two or more vectors. The parallelogram method or the triangle method can be used to find the product of two vectors.

Related Topics

• How to Find Vector Components
• How to Find Magnitude of Vectors
• How to Find Scalar Multiplication of Vectors
• Vectors Introduction

A step-by-step guide to vector addition and subtraction

To add or subtract two vectors, add or subtract the corresponding components.

If \(v⃗=(v_1,v_2)\) and \(u⃗ =(u_1,u_2)\)

Then, the sum of \( v⃗ \) and \(u⃗\) is the vector:

\(\color{blue}{v⃗ + u⃗ =(v_1+u_1, v_2+u_2)}\)

The difference of \( v⃗ \) and \(u⃗\) is:

\(\color{blue}{v⃗ – u⃗ = v⃗+( – u⃗ )=(v_1-u_1, v_2-u_2)}\)

The sum of two or more vectors is called the resultant. The parallelogram method or the triangle method can be used to find the product of two vectors.

Parallelogram Method:

Make sure the starting points of the vectors are the same. Then draw lines to form a parallelogram that is complete. The resultant is the diagonal that extends from the initial point to the parallelogram’s opposite vertex.

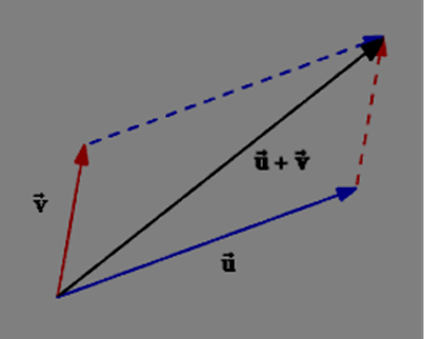
• Vector Addition:

1. Place both vectors \(u⃗\) and \(v⃗\) at the same beginning position in vector addition.
2. Complete the parallelogram. The parallelogram diagonal is represented by the resulting vector \(u⃗ +v⃗\).

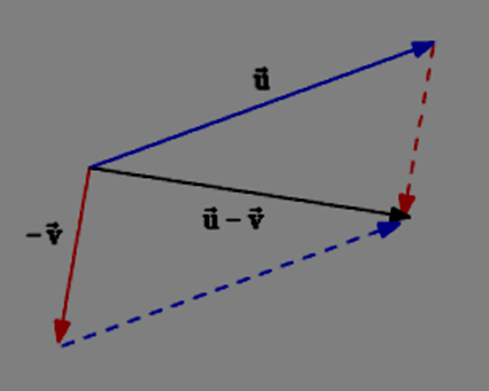
• Subtraction of vectors:

1. Fill in the blanks on the parallelogram.
2. Draw the parallelogram’s diagonals from the starting point.

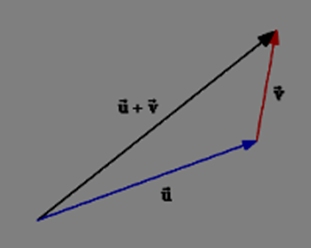
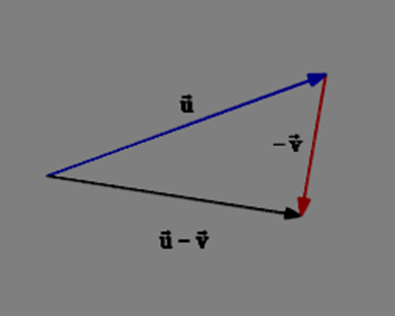
Method of the Triangle:

Draw the vectors one after the other, with the beginning point of each consecutive vector aligned with the preceding vector’s terminal point. Then draw the result from the first vector’s beginning point to the final vector’s terminal point. The “head-to-tail” approach is another name for this procedure.

• Addition of vectors:

• Vector Subtraction:

Vector Addition and Subtraction – Example 1:

If \(u⃗ =(4,3)\) and \(v⃗=(-1, 5)\), find \(u⃗ +v⃗\).

Use this formula to find the sum of vectors: \(\color{blue}{v⃗ + u⃗ =(v_1+u_1, v_2+u_2)}\).

\(u⃗ +v⃗=(4+(-1),3+5)\)

\(u⃗ +v⃗=(3,8)\)

Vector Addition and Subtraction – Example 2:

If \( v⃗ =(6,3)\) and \(u⃗=(-2, 5)\), find \(v⃗-u⃗ \).

First, we need to determine the components of \(− u⃗ \).  \(− u⃗ \) is a scalar multiple of \(−1\) times \(u\). From the definition of scalar multiplication we have:

\(−u⃗ =−1(u_1,u_2)\)

\(=-1(-2,5)\)

\(=(2,-5)\)

Now, add the components of \( v⃗ \) and \(−u⃗\).   

\( v⃗+ (-u⃗)=(6+2,3+(-5)\)

\(=(8,-2)\)

Exercises for the Vector Addition and Subtraction

1. Add the vectors v\(=(13, 8)\) and u\(=(7,26)\).
2. subtract vectors v\(=(4,5)\) from u\(=(12,2)\).
3. Add the vectors v\(=(14, 10)\) and u\(=(-6,16)\).
4. subtract vectors v\(=(-9,-6)\) from u\(=(-15,-3)\).
5. Add the vectors v\(=(2, -4)\) and u\(=(4,8)\).

1. \(\color{blue}{ v⃗+?⃗=(20,34)}\)
2. \(\color{blue}{ v⃗-?⃗=(-8,3)}\)
3. \(\color{blue}{ v⃗+?⃗=(8,26)}\)
4. \(\color{blue}{ v⃗-?⃗=(6,-3)}\)
5. \(\color{blue}{ v⃗+?⃗=(6,4)}\)