How to Understand Vectors: Vectors in Two Dimensions

Step-by-step Guide to Understand Vectors

Here is a step-by-step guide to understand vectors:

Step 1: Understanding the Basics

• Definition: A vector is a mathematical representation of both magnitude and direction. Think of it as an arrow pointing from one point to another.
• Components: In two dimensions, a vector has two parts: the \(x\)-component and the \(y\)-component, representing horizontal and vertical directions, respectively.

Step 2: Graphical Representation

• Axes Establishment: Start with a two-dimensional Cartesian plane. Label the horizontal axis as ‘\(x\)’ and the vertical axis as ‘\(y\)’.
• Drawing Vectors: Represent a vector as an arrow. The tail starts at the origin \((0,0)\) and the head (or tip) ends at the coordinate given by its \(x\) and \(y\) components.
• Length and Direction: The length of the arrow represents the magnitude of the vector. The direction in which it points gives, well, its direction.

Step 3: Defining Vectors Algebraically

• Notation: Typically, vectors are represented by bold letters or letters with an arrow above, like \(v\) or \(→v\).
• Components: A vector in \(2D\) can be written as \((x,y)\) or \(xi + yj\), where \(x\) and \(y\) are scalars and \(i\) and \(j\) are unit vectors in the \(x\) and \(y\) directions.

Step 4: Vector Operations

• Vector Addition: To add vectors, add their respective components. For vectors \(a = (x₁,y₁)\) and \(b = (x₂,y₂)\), the sum is \(a + b = (x₁+x₂, y₁+y₂)\).
• Vector Subtraction: Similarly, subtract the components: \(a – b = (x₁-x₂, y₁-y₂)\).
• Scalar Multiplication: Multiply each component of a vector by a scalar. For scalar \(k\) and vector \(a = (x,y), ka = (kx, ky)\).

Step 5: Magnitude and Direction

• Magnitude (or length): Given a vector \((x,y)\), its magnitude is found by the Pythagorean theorem: \(|v| = \sqrt{(x² + y²)}\).
• Direction: Using trigonometry, the angle \(θ\) (from the positive \(x\)-axis) is given by \(θ = tan⁻¹(\frac{y}{x})\).

Step 6: Unit Vectors

• Definition: A unit vector has a magnitude of one and points in a specific direction.
• In \(2D\): The primary unit vectors are \(i\) (which points in the positive \(x\)-direction) and \(j\) (which points in the positive \(y\)-direction).

Step 7: Dot Product

• Definition: It’s a way to multiply vectors resulting in a scalar. For vectors \(a = (x₁,y₁)\) and \(b = (x₂,y₂)\), the dot product is given by \(a • b = x₁x₂ + y₁y₂\).
• Orthogonal Vectors: If \(a • b = 0\), then vectors \(a\) and \(b\) are orthogonal (or perpendicular).

Step 8: Practical Applications

• Physics: Vectors are crucial in representing quantities like force, velocity, and acceleration.
• Computer Graphics: Used to describe positions, directions, and more, aiding in the creation of complex visualizations and animations.

Step 9: Beyond the Basics

• Once comfortable with vectors in two dimensions, expand your knowledge to three-dimensional vectors. Dive deeper into vector calculus, and explore concepts like cross-products and curl.

By taking a sequential, layered approach to vectors, you’ll build a robust foundation that can support more advanced mathematical and applied concepts. Vectors, though simple in concept, play a fundamental role in various disciplines, from physics to engineering to computer science. Dive in, explore, and let vectors guide your path through the intricate tapestry of mathematics.

Examples:

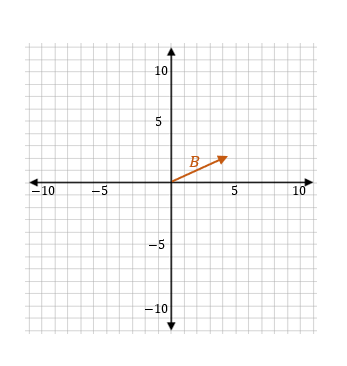
Show vector \(B=(4,2)\) in the coordinate plane.

Solution:

1. Setting up the Coordinate Plane:
   • Draw a set of perpendicular lines, the \(x\)-axis (horizontal) and the \(y\)-axis (vertical). These represent your coordinate plane.
   • Mark intervals on each axis, similar to a grid, to denote units.
2. Plotting the Vector:
   • Start at the origin, the point \((0,0)\).
   • Move \(4\) units to the right along the \(x\)-axis. This represents the \(x\)-component of the vector.
   • From that point, move \(2\) unit upwards. This represents the \(y\)-component of the vector.
   • Draw an arrow starting from the origin to the point you’ve reached, which is \((4,2)\). The arrow represents vector \(B\).