Full-Length 8th Grade ACT Aspire Math Practice Test-Answers and Explanations
Did you take the 8th Grade ACT Aspire Math Practice Test? If so, then it’s time to review your results to see where you went wrong and what areas you need to improve.
8th Grade ACT Aspire Math Practice Test Answers and Explanations
1- Choice C is correct
The weight of 12.2 meters of this rope is: 12.2 × 600 g = 7320 g
1kg = 1000 g, therefore, 7320 g ÷ 1000 = 7.32 kg
2- The correct answer is 600.
The ratio of boys to girls is 3 : 7. Therefore, there are 3 boys out of 10 students. To find the answer, first divide the number of boys by 3, then multiply the result by 10.
180 ÷ 3 = 60 ⇒ 60 × 10 = 600
3- Choice C is correct.
the population is increased by \(15\%\) and \(20\%\). \(15\%\) increase changes the population to \(115\%\) of original population.
For the second increase, multiply the result by \(120\%\).
\((1.15) × (1.20) = 1.38 = 138\%\)
38 percent of the population is increased after two years.
4- Choice A is correct.
Let \(x\) be the number of new shoes the team can purchase. Therefore, the team can purchase 240 \(x\).
The team had $40,000 and spent $22,000. Now the team can spend on new shoes $18,000 at most.
Now, write the inequality: \(120x+22.000 ≤40.000\)
5- Choice B is correct.
A linear equation is a relationship between two variables, \(x\) and \(y\), that can be put in the form \(y = mx + b\).
A non-proportional linear relationship takes on the form \(y = mx + b\), where b ≠ 0 and its graph is a line that does not cross through the origin.
6- Choice C is correct
The perimeter of the rectangle is: \(2x+2y=30→x+y=15→x=15-y\)
The area of the rectangle is: \(x×y=50→(15-y)(y)=50→y^2-15y+50=0\)
Solve the quadratic equation by factoring method.
\((y-5)(y-10)=0→y=5\) (Unacceptable, because y must be greater than 5) or \(y=10\)
If \(y=10 →x×y=50→x×10=50→x=5\)
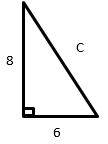
7- The correct answer is 10.
Use the information provided in the question to draw the shape.
Use Pythagorean Theorem: \(a^2 + b^2 = c^2\)
\(6^2 + 8^2 = c^2 ⇒ 100 = c^2 ⇒ c = 10\)
8- Choice D is correct
\(3x-5=8.5→3x=8.5+5=13.5→x=\frac{13.5}{3}=4.5\)
Then; \(5x+3=5 (4.5)+3=22.5+3=25.5\)
9- The correct answer is 1,800.
Use simple interest formula: I=prt (I = interest, p = principal, r = rate, t = time)
\(I=(8000)(0.045)(5)=1800\)
10- Choice C is correct.
Let \(x\) be the number of soft drinks for 252 guests. Write the proportion and solve for \(x\).
\(\frac{10 \space soft \space drinks}{12 \space guests}=\frac{x}{252 \space guests}\)
\(x =\frac{252×10}{12} ⇒x=210\)
The Absolute Best Book to Ace the 8th Grade ACT Aspire Math Test
ACT Aspire Grade 8 Mathematics A Comprehensive Review and Ultimate Guide to the ACT Aspire Math Test
11- Choice C is correct
\(4\%\) of the volume of the solution is alcohol. Let \(x\) be the volume of the solution.
Then: \(4\%\) of \(x = 24\) ml ⇒ \(0.04 x = 24 ⇒ x = 24 ÷ 0.04 = 600\)
12- The correct answer is 40.
Use the area of rectangle formula \((s = a × b)\).
To find area of the shaded region subtract smaller rectangle from bigger rectangle.
\(S_1 – S_2 = (10 \space ft × 8 \space ft) – (5 \space ft × 8 \space ft) ⇒ S_1 – S_2 = 40 \space ft\)
13- Choice B is correct
Use the formula for Percent of Change
\(\frac{New \space Value-Old \space Value}{Old \space Value}
× 100\%\)
\(\frac{28-40}{40} × 100 \% = –30 \%\) (negative sign here means that the new price is less than old price).
14- The correct answer is 1,000.
Use simple interest formula: I=prt (I = interest, p = principal, r = rate, t = time)
\(I=(5000)(0.05)(4)=1,000\)
15- The answer is 8.
Use formula of rectangle prism volume. V = (length) (width) (height) ⇒ 2000 = (25) (10) (height) ⇒ height = 2000 ÷ 250 = 8
16- Choice B is correct.
Use this formula: Percent of Change
\(\frac{New \space Value-Old \space Value}{Old \space Value}
× 100\%\)
\(\frac{16,000-20,000}{20,000} × 100\% = 20\% \space and \space \frac{12,800-16,000}{16000} × 100\% = 20\%\)
17- The correct answer is 62.8.
To find the area of the shaded region subtract smaller circle from bigger circle.
\(S_ {bigger} – S_ {smaller} = π (r _{bigger} )^2 – π (r _{smaller} )^2 ⇒ S _{bigger} – S _{smaller} = π (6)^2 – π (4)^2\)
\(⇒ 36 π – 16π = 20 π = 20 × 3.14 = 62.8\)
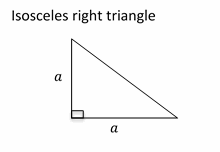
18- The answer is 18.
\(a=6\)⇒ area of the triangle is \(=\frac{1}{2}(6×6)=\frac{36}{2}=18 \space cm^2\)
19- Choice C is correct
\($9×10=$90\)
Petrol use: \(10×2=20\) liters
Petrol cost: \(20×$1=$20\)
Money earned: \($90-$20=$70\)
20- The answer is 20.
Five years ago, Amy was three times as old as Mike. Mike is 10 years now. Therefore, 5 years ago Mike was 5 years.
Five years ago, Amy was: \(A=3×5=15\)
Now Amy is 20 years old: \(15 + 5 = 20\)
21- Choice D is correct
\(\begin{cases}\frac{-x}{2}+\frac{y}{4}=1\\\frac{-5y}{6}+2x=4\end{cases}\)
Multiply the top equation by 4. Then,
\(\begin{cases}-2x+y=4\\\frac{-5y}{6}+2x=4\end{cases}\)
→ Add two equations.
\(\frac{1}{6}y=8→y=48\) , plug in the value of y into the first equation →\(x=22\)
22- The answer is 4.8.
Two triangles ∆BAE and ∆BCD are similar. Then:
\(\frac{AE}{CD}=\frac{AB}{BC}→\frac{4}{6}=\frac{x}{12}→48-4x=6x→10x=48→x=4.8\)
23- Choice D is correct
\(\frac{2}{5}×25=\frac{50}{5}=10\)
24- Choice D is correct
The slop of line A is: \(m=\frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{4-3}=1\)
Parallel lines have the same slope and only choice D \((y=x)\) has slope of 1.
25- The answer is 5.
\(x\) is directly proportional to the square of \(y\). Then:
\(x=cy^2\)
\(12=c(2)^2→12=4c→c=\frac{12}{4}=3\)
The relationship between \(x\) and \(y\) is: \(x=3y^2, x=75\), \(75=3y^2→y^2=\frac{75}{3}=25→y=5\)
26- The answer is 54.
The amount of money that jack earns for one hour: \(\frac{$616}{44}=$14\)
Number of additional hours that he work to make enough money is: \(\frac{$826-$616}{1.5×$14}=10\)
Number of total hours is: \(44+10=54\)
27- Choice C is correct
Let’s find the mean (average), mode and median of the number of cities for each type of pollution.
Number of cities for each type of pollution: 6, 3, 4, 9, 8
??????? (????) \(=\frac{sum \space of \space terms}{number \space of \space terms}= \frac{6+3+4+9+8}{5}=\frac{30}{5}=6\)
Median is the number in the middle. To find median, first list numbers in order from smallest to largest.
3, 4, 6, 8, 9
Median of the data is 6.
Mode is the number which appears most often in a set of numbers. Therefore, there is no mode in the set of numbers.
Median = Mean, then, ? = ?
28- Choice A is correct
Percent of cities in the type of pollution A: \(\frac{6}{10}×100=60\%\)
Percent of cities in the type of pollution C: \(\frac{4}{10}0×100=40\%\)
Percent of cities in the type of pollution E: \(\frac{9}{10}×100=90\%\)
29- The answer is 2.
Let the number of cities should be added to type of pollution’s B be \(x\). Then: \(\frac{x+3}{8}=0.625→x+3=8×0.625→x+3=5→x=2\)
30- Choice A is correct
AB = 12 and AC = 5
\(BC=\sqrt{12^2+5^2}=\sqrt{144+25}=\sqrt{169}=13\)
Perimeter \(=5+12+13=30\)
Area \(=\frac{5×12}{2}=5×6=30\)
In this case, the ratio of the perimeter of the triangle to its area is: \(\frac{30}{30}=1\)
If the sides AB and AC become twice longer, then:
AB = 24 and AC = 10
BC \(=\sqrt{24^2+10^2}=\sqrt{576+100}=\sqrt{676}=26\)
Perimeter \(=26+24+10=60\)
Area \(=\frac{10×24}{2}=10×12=120\)
In this case the ratio of the perimeter of the triangle to its area is: \(\frac{60}{120}=\frac{1}{2}\)
Best 8th Grade ACT Aspire Math Prep Resource for 2022
31- The answer is 25.
The capacity of a red box is \(20\%\) bigger than the capacity of a blue box and it can hold 30 books. Therefore, we want to find a number that \(20\%\) bigger than that number is 30. Let \(x\) be that number. Then:
\(1.20×x=30\), Divide both sides of the equation by 1.2. Then:
\(x=\frac{30}{1.20}=25\)
32- Choice C is correct
The smallest number is \(-15\). To find the largest possible value of one of the other five integers, we need to choose the smallest possible integers for four of them. Let x be the largest number. Then:
\(-70=(-15)+(-14)+(-13)+(-12)+(-11)+x→-70=-65+x →x=-70+65=-5\)
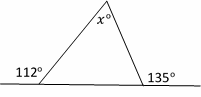
33- The answer is 67.
\(α=180\circ -112\circ=68\circ\)
\(β=180\circ-135\circ=45\circ\)
\(x+α+β=180\circ→x=180\circ-68\circ-45\circ=67\circ\)
34- Choice D is correct
A. \(f(x)=x^2-5\) →if \(x=1→f(1)=(1)^2-5=1-5=-4≠5\)
B. \(f(x)=x^2-1\) →if \(x=1→f(1)=(1)^2-1=1-1=0≠5\)
C. \(f(x)=\sqrt{x+2}\)→ if \(x=1→f(1)=\sqrt{1+2}=\sqrt{3}≠5\)
D. f(x)=\sqrt{x}+4 \) →if \(x=1→f(1)=\sqrt{1}+4=5\)
35- The answer is $810.
Let \(x\) be all expenses, then \(\frac{22}{100} x=$660 →x=\frac{100×$660}{22}=$3000\)
He spent for his rent: \(\frac{27}{100}×$3000=$810\)
36- Choice C is correct
The amount of money for \(x\) bookshelf is: \(100x\)
Then, the total cost of all bookshelves is equal to: \(100x+800\)
The total cost, in dollar, per bookshelf is: \(\frac{Total \space cost}{number \space of \space items}=\frac{100x+800}{x}\)
37- The answer is 0.
\(\sqrt{x}=4→x=16\)
then; \(\sqrt{x}-7=\sqrt{16}-7=4-7=-3\) and \(\sqrt{x-7}=\sqrt{16-7}=\sqrt{9}=3\)
Then: \((\sqrt{x-7})+(\sqrt{x}-7)=3+(-3)=0\)
38- Choice B is correct
The angles on a straight line add up to 180 degrees. Then: \(x+25+y+2x+y=180\)
Then, \(3x+2y=180-25→3(35)+2y=155\)
\(→2y=155-105=50→y=25\)
39- Choice C is correct
Square root of 16 is \(\sqrt{16}=4<6\) Square root of 25 is \(\sqrt{25}=5<6 \) Square root of 37 is \(\sqrt{37}=\sqrt{36+1}>\sqrt{36}=6\)
Square root of 49 is \(\sqrt{49}=7>6\)
Since, \(\sqrt{37}<\sqrt{49}\), then the answer is C.
40- The answer is 11.
\(|-12-5|-|-8+2|=|-17|-|-6|=17-6=11\)
41- Choice C is correct
A probability is the likelihood of a successful event occurring divided by the total number of events possible. In this case, a successful event is selecting either a red or a yellow marble and the total number of events possible is the total number of marbles. Combine the number of red and yellow marbles: 8 + 5 = 13, and divide this by the total number of marbles: 6 + 8 + 5 = 19. The probability is 13 out of 19.
42- Choice C is correct
A factor must divide evenly into its multiple. 14 cannot be a factor of 80 because 80 divided by 16 = 5.71
43- The answer is 16.
The total cost of the phone call can be represented by the equation:
\(TC = $4.00 + $0.4x\), where \(x\) is the duration of the call after the first five minutes. In this case, \(x = 30\). Substitute the known values into the equation and solve: \(TC = $4.00 + $0.4 × 30\)
\(TC = $4.00 + $12.00 , TC = $16.00\)
44- Choice C is correct
Find the difference of the two expression: \((5x+8)-(5x-3)=5x+8-5x+3=11\)
45- The answer is 45.
First, find the number. Let \(x\) be the number. Write the equation and solve for \(x\). \(150\%\) of a number is 75, then:
\(1.5×x=75→x=75÷1.5=50, 90\%\) of 50 is: \(0.9×50=45\)
46- Choice A is correct
The length of MN is equal to: \(3x+5x=8x, Then: 8x=40→x=\frac{40}{8}=5\)
The length of ON is equal to: \(5x=5×5=25\) cm
47- Choice A is correct
The general slope-intercept form of the equation of a line is \(y = mx + b\), where \(m\) is the slope and \(b\) is the \(y\)-intercept. By substitution of the given point and given slope, we have:
\(-2 = (2)(7) + b\), So, \(b = –2 – 14 = -6\), and the required equation is \(y = 2x – 16\).
48- Choice D is correct
Multiplying each side of \(-3x-y=6\) by \(2\) gives \(-6x -2y = 12\). Adding each side of \(-6x – 2y = 12\) to the corresponding side of \(6x+4y=10\) gives \(2y=22\) or \(y=11\). Finally, substituting \(11\) for \(y\) in \(6x+4y=10\) gives \(6x+4(11)=10\) or \(x=-\frac{17}{3}\).
49- Choice B is correct
\(x_{1,2} =\frac{-b ± \sqrt{b^2-4ac}}{2a}\) ,
\( ax^2 + bx + c = 0, 4x^2 + 14x + 6 = 0 \) ⇒ then: \(a = 4\), \(b = 14\) and \(c = 6\),
\(x = \frac{-14 +\sqrt{14^2 – 4 .4 .6}}{2.4} = – \frac{1}{2}, x =\frac{-14 – \sqrt{14^2 – 4 .4 .6}}{2.4} = – 3\)
50- Choice A is correct
Use Pythagorean theorem: \(a^2+b^2=c^2→s^2+h^2=(5s)^2→s^2+h^2=25s^2\)
Subtracting s^2 from both sides gives: \(h^2=24s^2\)
Square roots of both sides: \(h=\sqrt{24s^2}=\sqrt{4×6×s^2} =\sqrt{4}×\sqrt{6}×\sqrt{s^2 }=2×s×\sqrt{6}=2s\sqrt{6}\)
51- Choice D is correct
Let \(x\) be the number of purple marbles. Let’s review the choices provided:
A. \(\frac{1}{10}\), if the probability of choosing a purple marble is one out of ten, then:
Probability \(=\frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}=\frac{x}{20+30+40+x}=\frac{1}{10}\)
Use cross multiplication and solve for \(x\).
\(10x=90+x→9x=90→x=9\)
Since, number of purple marbles can be 9, then, choice be the probability of randomly selecting a purple marble from the bag.
Use same method for other choices.
B. \(\frac{1}{4}\)
\(\frac{x}{20+30+40+x}=\frac{1}{4}→4x=90+x→3x=90→x=30\)
C. \(\frac{2}{5}\)
\(\frac{x}{20+30+40+x}=\frac{2}{5}→5x=180+2x→3x=180→x=60\)
D. \(\frac{7}{15}\)
\(\frac{x}{20+30+40+x}=\frac{7}{15}→15x=630+7x→8x=630→x=78.75\)
Number of purple marbles cannot be a decimal.
52- Choice C is correct
Area = w × h
Area = 138 × 83 = 11,454
53- Choice D is correct
\(4x^2y^3 + 5x^3y^5 – (5x^2y^3 – 2x^3y^5) = 4x^2y^3 + 5x^3y^5 – 5x^2y^3 + 2x^3y^5 = – x^2y^3 + 7x^3y^5\)
The Best Books to Ace the 8th Grade ACT Aspire Math Test
Common Core Math Exercise Book for Grade 8 Student Workbook and Two Realistic Common Core Math Tests
ACT Aspire Grade 8 Mathematics A Comprehensive Review and Ultimate Guide to the ACT Aspire Math Test
Related to This Article
More math articles
- ACT Math Test-Taking Strategies
- Top 10 Tips to Create an ISEE Math Study Plan
- 6th Grade RICAS Math Worksheets: FREE & Printable
- How to Solve Finite Geometric Series? (+FREE Worksheet!)
- Understanding Trigonometry: How to Calculate the Area of Triangles
- Number Properties Puzzle – Challenge 22
- Is ALEKS just for Mathematics?
- Is ALEKS a Good Mathematics Program?
- Model Magic: Visualizing Division with Two-digit Divisors
- The Best Keyboards For Online Teaching
What people say about "Full-Length 8th Grade ACT Aspire Math Practice Test-Answers and Explanations - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.