How to Find Scalar Multiplication of Vectors?
[include_netrun_products_block from-products="product/10-full-length-pert-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{{url}}/?ajax-add-to-cart={{id}}" product-item-button-custom-url-if-not-salable="{{productUrl}} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
To multiply a vector by a scalar, multiply each component by a scalar. The product of a scalar with a vector is always a vector.
Related Topics
A step-by-step guide to scalar multiplication of vectors
The scalar component of the vector is multiplied by the scalar component of each component of the vector.
If \(u⃗=(u_1, u_2)\) has a magnitude of \(|u⃗ |\) and a direction of \(d\), then:
\(\color{blue}{|nu⃗ |=n(u_1,u_2)=(nu_1,nu_2)}\)
where \(n\) is a positive real integer, the magnitude is \(|nu⃗ |\) and the direction is \(d\).
If \(n\) is negative, the direction of \(n\)u is the total opposite of \(d\).
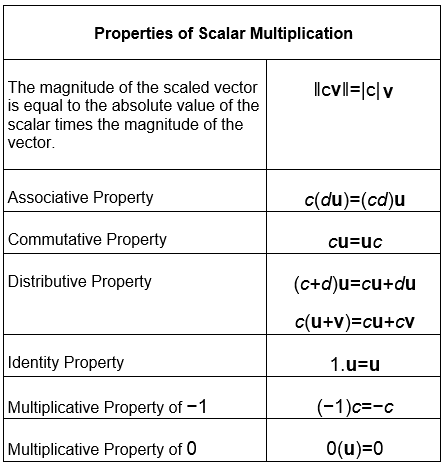
Properties of Scalar Multiplication:
Allow u and v to be vectors, and \(c\) and \(d\) to be scalars. Then the properties listed below are true:
Scalar Multiplication of Vectors – Example 1:
If u\(=(-2, 3)\), find \(6\)u.
\(6\)u\(=6(-2,3)\)
\(=6(-2),6(3)\)
\(=(-12,18)\)
Scalar Multiplication of Vectors – Example 2:
If a\(=3i+j+2k\), find \(5\)a.
\(5\)a\(=5(3i+j+2k)\)
\(=5(3i)+5(j)+5(2k)\)
\(=15i+5j+10k\)
Exercises for Scalar Multiplication of Vectors
- If a\(=(-1,-8)\), find \(4\)a.
- If v\(=6i-5j+4k\), find \(3\)v.
- If a\(=7, -3\), find \(-5\)a.
- If v\(=i-7j-5k\), find \(-6\)v.
- \(\color{blue}{4a=(-4,-32)}\)
- \(\color{blue}{3v=18i-15j+12k}\)
- \(\color{blue}{-5a=(-35,15)}\)
- \(\color{blue}{-6v=-6i+42j+35k}\)
Related to This Article
More math articles
- 7th Grade MEA Math Worksheets: FREE & Printable
- 4th Grade MCA Math Worksheets: FREE & Printable
- How to Find Vector Components?
- Overview of the ACT Mathematics Test
- What Is the Best GED Math Study Guide?
- 5 Best Math Books for College Students: A Comprehensive Review
- Where to Go to Get Math Homework Help Quickly and Effectively?
- FREE 6th Grade Common Core Math Practice Test
- ACT Tеѕting Accommodations fоr Studеntѕ with Diѕаbilitiеѕ
- 8th Grade DCAS Math Worksheets: FREE & Printable
What people say about "How to Find Scalar Multiplication of Vectors? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.