How to Graph Lines by Using Slope–Intercept Form? (+FREE Worksheet!)
Learn how to graph lines using the equation of the line in slope-intercept form.
Related Topics
- How to Find Midpoint
- How to Find Slope
- How to Graph Linear Inequalities
- How to Write Linear Equations
- How to Graph Lines by Using Standard Form
Step by step guide to graphing lines using slope–intercept form
- Slope–intercept form of a line: given the slope \(m\) and the \(y\)–intercept (the intersection of the line and \(y\)-axis) \(b\) , then the equation of the line is:
\(y=mx+b\)
The Absolute Best Books to Ace Pre-Algebra to Algebra II
Graphing Lines Using Slope–Intercept Form – Example 1:
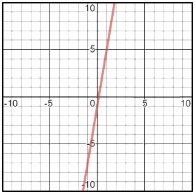
Sketch the graph of \(y=6x-1\)
Solution:
To graph this line, we need to find two points. When \(x\) is zero the value of \(y\) is \(-1\). And when \(y\) is zero the value of \(x\) is \(\frac{1}{6}\).
\(y=6x-1\) → \(x=0→y=6(0)-1 → y= \ – \ 1\)
\(y=6x-1 → y=0→0=6x-1→x=\frac{1}{6}\)
Now, we have two points: \((0,-1)\) and \((\frac{1}{6},0)\). Find the points and graph the line. Remember that the slope of the line is \(6\).
Graphing Lines Using Slope–Intercept Form – Example 2:
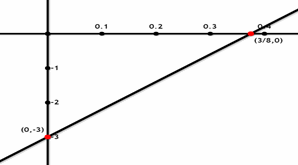
Sketch the graph of \(y=8x-3\).
Solution:
To graph this line, we need to find two points. When \(x\) is zero the value of \(y\) is \(-3\). And when \(y\) is zero the value of \(x\) is \(\frac{3}{8}\).
\(y=8x-3\) → \(x=0→y=8(0)-3 → y=-3\)
\(y=8x-3 → y=0→0=8x-3→x=\frac{3}{8}\)
Now, we have two points: \((0,-3)\) and \((\frac{3}{8},0)\). Find the points and graph the line. Remember that the slope of the line is \(8\).
Exercises for Graphing Lines Using Slope–Intercept Form
Sketch the graph of each line.
- \(\color{blue}{y = \frac{1}{ 2} x – 4}\)
- \(\color{blue}{y = 2x}\)
Download Graphing Lines Using Line Equation Worksheet
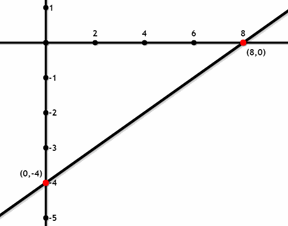
- \(\color{blue}{y = \frac{1}{ 2} x – 4}\)
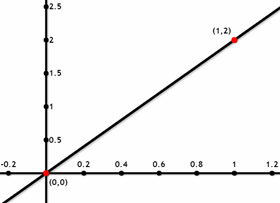
- \(\color{blue}{y = 2x}\)
The Greatest Books for Students to Ace the Algebra
Related to This Article
More math articles
- Top Calculators for the GED 2023: Quick Review
- Division Dynamics: How to Solve Word Problems with Multi-digit Dividends and One-digit Divisors!”
- How to Teach the GED Math Effectively: A Complete Guide!
- How to Solve the Ambiguous Case (SSA) in Trigonometry
- How to Find the Domain and Range of Quadratic Functions
- How to Use Comparison test for Convergence
- FREE 5th Grade Common Core Math Practice Test
- Quadratic Function
- Top 10 Tips to ACE the ACT Mathematics
- Best Cameras For Classroom Video Lectures And Online Lessons
What people say about "How to Graph Lines by Using Slope–Intercept Form? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.