What is the difference between LCM and HCF and how to calculate these properly?
The highest common factor and least common multiple are such concepts that are important not only for the school level but also for several exams.
These exams might be MAT, CAT, and different recruitment exams.
So, it is important to understand the basic concepts and properties of these two properly.
In this article, we’re going to discuss what is LCM and HCF, their properties & differences, and how to calculate these properly with suitable examples.
What are LCM and HCF?
LCM is the smallest whole number that occurs in both of their time tables and it is the smallest integer that is a multiple of both numbers.
It is also known as the lowest common multiple and shows the least number divisible by 2 or more numbers.
For example, suppose two numbers 4 and 5.
The common multiples of 4 are:
4, 8, 12, 16, 20, 24, 28
And of 5 are:
5, 10, 15, 20, 25.
The LCM of two different numbers 4 & 5 is 20.
Whereas, HCF is the highest common factor between different numbers.
It is the largest number that divides two or more than two numbers.
It is also known as the greatest common factor and can be found by several new methods.
For example, suppose two numbers ‘30’ and ‘36’.
The factors for 30 is (2 x 3 x 5) and for 36 (2 x 2 x 3 x 3).
The HCF of these two numbers is 6 because it is the biggest number that divides each of these numbers.
The Absolute Best Book for the Algebra I
Difference between HCF and LCM
LCM is the least common multiple and HCF is the highest common factor between different numbers.
The main purpose of showing the difference between these two numbers is to show the difference between a factor and a multiple.
A multiple of a whole number is an integer that occurs in the timetable.
For example, let’s have a look at the multiples of 3:
3, 6, 9, 12, 15, 18, and so on.
Whereas, the factor of an integer is that number that divides the integer with no reminder at the end.
For example, let’s have a look at the factors of 36:
1, 2, 3, 4, 6, 9, 12, 18, and 36.
To find the relation between the LCM and HCF of two different numbers first, we need to find the highest common factor of 15 and 18 which is 3.
And the exact LCM of 15 and 18 is 90.
L.C.M x H.C.F = 90 X 3 = 270
Whereas the product of these two numbers is,
15 x 18 = 270
Thus, the product of L.C.M and H.C.F is equal to the product of these two numbers.
Properties of LCM and HCF
Some of the main properties of these two concepts are:
- The highest common factor of two or more two prime numbers is always 1.
- The LCM of two or more than two numbers will be their products.
- The HCF of the given numbers is never greater than the given numbers.
- The least common multiple of the given numbers is never smaller than any of the given numbers
- The product of two different numbers ‘a’ and ‘b’ is always equal to the
product of their least common multiples and HCF.
Further in this article, we’ll discuss that:
How to Calculate HCF and LCM properly?
You can use the mentioned below ways to calculate the LCM or HCF of two numbers:
⦁ Prime Factorization Method for LCM and HCF
To calculate the least common factor of random two numbers 45 and 60 simply follow the:
- List the prime factors of the given numbers as:
45 = 2 x 2 x 3 x 5
60 = 3 x 3 x 5 - Multiply each factor that occurs for the maximum number of times
LCM = 2 x 2 x 3 x 3 x 5 = 180.
To calculate the HCF by the prime factorization method take two random numbers 104 and 144.
The prime factors of these two numbers are:
104 = 23 x 13
144 = 2 x 2 x 2 x 2 x 3 x 3
The most common factors of these two numbers are 2 x 2 x 2.
So, the HCF of the given numbers is:
HCF = 2 x 2 x 2 = 8.
⦁ Division Method for LCM and HCF
To calculate the least common multiple “LCM” of two different numbers 24 and 15, follow the mentioned below steps:
- Divide the given number by the lowest prime number
- Write the number and quotient that are not divisible by the least prime number
- Further, divide these numbers with the other prime number
- Keep the division number until the reminder becomes the prime number or 1.
- Multiply the divisors and other prime numbers to get the LCM.
The LCM of the two numbers 24 and 15 is:
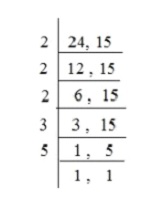
LCM of these two numbers is:
LCM = 2 x 2 x 2 x 3 x 5 = 120.
To calculate HCF by division method, simply follow the mentioned below steps:
- Divide the larger number by the smaller one
- Further, divide the divisor of the above one by the reminder
- Keep dividing the divisor of step 2 with the reminder until the remainder becomes zero.
For example, suppose two different numbers 12 and 18.
The greatest common factor of these numbers is:
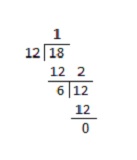
The HCF of these two numbers by the division method is 6.
The Absolute Best Book for the Algebra Test
⦁ Using Online Calculators
Several useful online calculators are available to find the greatest common factor.
These converters allow you to check the HCF, LCM, or GCD of different numbers with just a single click.
These online calculators also allow you to select the desired method to find the LCM or HCF.
Most of the tools provide the following methods to check the highest common factor and least common multiple:
- Prime Factorization Method
- Division Method
- Euclidean Method
- Binary Stein’s Algorithm
- And more
The Best Books to Ace Algebra
Related to This Article
More math articles
- A Comprehensive Collection of Free TASC Math Practice Tests
- How to Multiply Exponents? (+FREE Worksheet!)
- The Ultimate Adults Algebra Refresher Course (+FREE Worksheets & Tests)
- The Best School Supplies for Learning Math
- OAR Math Practice Test Questions
- Best SAT Math Prep Books
- The Ultimate MTEL Mathematics (Elementary) (68) Course (+FREE Worksheets & Tests)
- The Ultimate PSAT 10 Math Course (+FREE Worksheets & Tests)
- 10 Most Common 7th Grade NYSE Math Questions
- The Best Scientific Calculator to Buy for School and Work
What people say about "What is the difference between LCM and HCF and how to calculate these properly? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.