How to Find Vertical Angles? (+FREE Worksheet!)

In this article, you will learn how to Find Vertical angles in a few simple steps.
Step by step guide to Finding Vertical angles
The intersecting lines form an \(X\)-shape, and the angles on the two opposite sides of this \(X\) are called vertical angles. The two vertical angles are always the same size and they have the same vertex. The bisector of two vertical angles makes a straight angle.
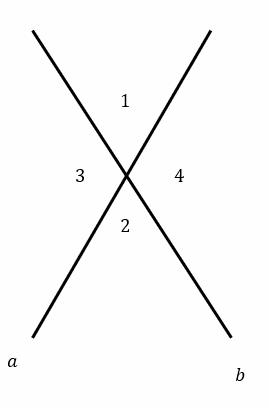
In the diagram at the right, lines and are straight:
- Angle\(1\)+ Angle\(3\)=\(180\)(because it is a straight angle)
- Angle\(2\)+ Angle\(3\)=\(180\)(because it is a straight angle)
Infer from the above two relations that angle \(1\) and \(2\) angle are equal; So, the vertical angles are equal.
In this diagram:
- Angle \(1\) and angle \(2\) are vertical angles.
- Angle \(3\) and angle \(4\) are vertical angles.
- Angle \(1\) and angle \(3\) are NOT vertical angles.
Finding Vertical Angles Example 1:
Find the number of degrees.
Solution: \((3x+50)^{\circ}\) and \((5x+10)^{\circ}\) are vertical angles.
\(3x+50=5x+10→3x+50-50=5x+10-50→3x=5x-40→3x-5x=-40→-2x=-40→x=20\)
\((3x+50)^{\circ}=(3(20)+50)=110^{\circ}\)
\((5x+10)^{\circ}=(5(20)+10=110^{\circ}\)
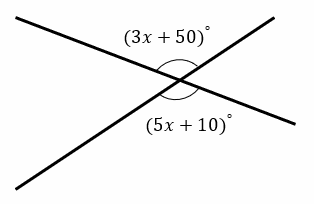
Finding Vertical Angles Example 2:
Find the number of degrees.
Solution: \((4x)^{\circ}\) and \((6x-22)^{\circ}\) are vertical angles.
\(4x=6x-22→4x-6x=-22→-2x=-22→x=11\)
\((4x)^{\circ}=(4(11))=44^{\circ}\)
\((6x-22)^{\circ}=(6(11)-22=44^{\circ}\)
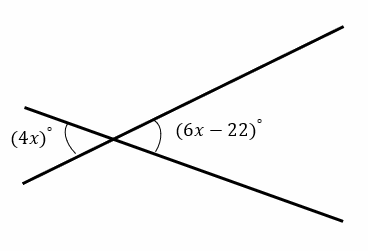
Exercises for Finding Vertical Angles
Find the value of \(x\).
1)
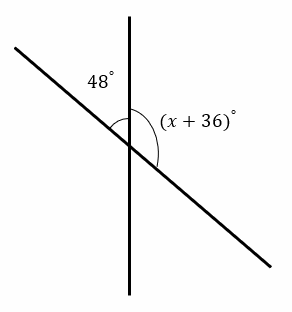
2)
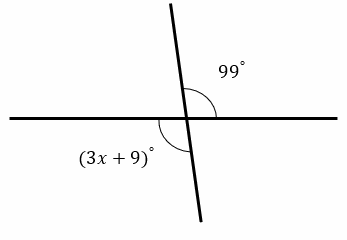

- \(x=96\)
- \(x=30\)
Related to This Article
More math articles
- How to Understand the Concept of Scale Changes: Area and Perimeter
- Ratio, Proportion and Percentages Puzzle -Critical Thinking 10
- 10 Most Common 4th Grade ACT Aspire Math Questions
- A Comprehensive Collection of Free ALEKS Math Practice Tests
- How Is the ALEKS Test Scored?
- Math Courses Required For A Business Degree
- How to Solve Inverse Trigonometric Functions?
- How to Prepare for the ASTB Math Test?
- Best Laptops for Back to School
- Top 10 TExES Core Subjects EC-6 Math Practice Questions


























What people say about "How to Find Vertical Angles? (+FREE Worksheet!) - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.