How to Find Vector Components?

The components of a vector give a split of the vector. The vector is split according to each of the axes and we can calculate the components of a vector.

Related Topics

• Vectors Introduction
• How to Find Magnitude of Vectors
• How to Find Scalar Multiplication of Vectors

A step-by-step guide to vector components

• Any vector in a two-dimensional coordinate system can be broken down into its \(x\) and \(y\)-components.

\(v⃗ =(v_x,v_y)\)

For example, in the picture given below, the vector \(v⃗\) is divided into two components, \(v_x\) and \(v_y\). Let the angle between the vector and its \(x\)-component be \(θ\).

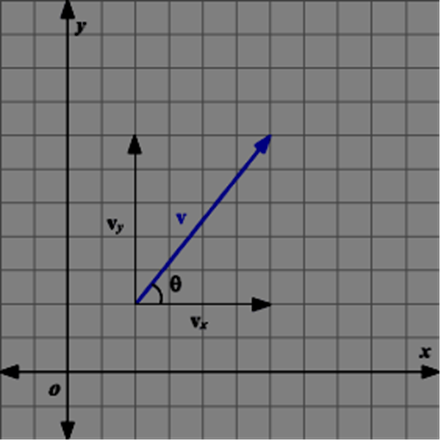
In the diagram below, the vector and its component form a right-angled triangle:

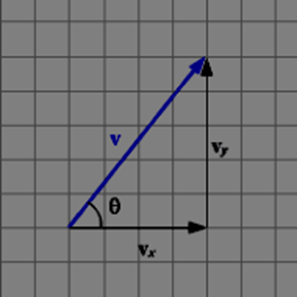
In the above figure, the components can be easily and quickly read. The vector in the component form is \(v⃗ =(4,5)\).

• Trigonometric ratios show the relationship between the magnitude of the vector and the components of the vector.

\(\color{blue}{cos θ=\frac{v_x}{v}}\) → \(\color{blue}{v_x= v \cos θ}\)

\(\color{blue}{sin θ=\frac{v_y}{v}}\) → \(\color{blue}{v_y= v \sin θ}\)

• Using “Pythagoras theorem” in right triangles with lengths \(v_x\) and \(v_y\):

\(\color{blue}{|v|=\sqrt{v_x^2+v_y^2}}\)

Note1:

Find the magnitude and direction of the vector with respect to the components of a vector. In this case, use the following formulas:

The magnitude of the vector is \(\color{blue}{|v|=\sqrt{v_x^2+v_y^2}}\).

To find the direction of the vector, solve \(\color{blue}{tan θ=\frac{v_y}{v_x}}\) for \(θ\).

Note 2:

Find the components of a vector according to the magnitude and direction of a vector. In this case, use the following formulas:

\(\color{blue}{v_x= v \cos θ}\)

\(\color{blue}{v_y= v \sin θ}\)

Vector Components – Example 1:

The magnitude of a vector \(v⃗\) is \(20\) units and the direction of the vector is \(60°\) with the horizontal. Find the components of the vector.

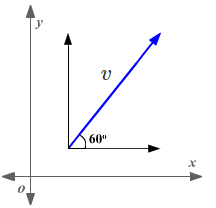
To find the components of a vector use these formulas:

\(\color{blue}{v_x= v \cos θ}\)

\(\color{blue}{v_y= v \sin θ}\)

\(v_x= v\cos 60° \) → \(v_x= 20×\frac{1}{2}= \frac{20}{2}=10\)

\(v_y= v\sin 60° \) → \(v_y= 20×\frac{\sqrt{3}}{2}= \frac{20\sqrt{3}}{2} =10\sqrt{3}\)

So, the vector \(v⃗\) is \((10, 10\sqrt{3})\).

Vector Components – Example 2:

Find the \(x\) and \(y\) components of a vector having a magnitude of \(10\) and make an angle of \(45\) degrees with the positive \(x\)-axis.

To find the components of a vector use these formulas:

\(\color{blue}{v_x= v \cos θ}\)

\(\color{blue}{v_y= v \sin θ}\)

\(v_x= v\cos 45° \) → \(v_x= 10×\frac{\sqrt{2}}{2}= \frac{10\sqrt{2}}{2} =5\sqrt{2}\)

\(v_y= v\sin 45° \) → \(v_y= 10×\frac{\sqrt{2}}{2}= \frac{10\sqrt{2}}{2} =5\sqrt{2}\)

So, the \(x\)-component and the \(y\)-components of the vector are both equal to \(5\sqrt{2}\).

Exercises for Vector Components

1. Find the value of \( θ \), if \(v_x=15\) and \(v_y=8.66\).
2. Find out the magnitude of a vector \(OA=(-3,4)\).
3. Find the components of the vector, if the magnitude of a vector \(v⃗\) is \(6\) units and the direction of the vector is \(30°\) with the horizontal.
4. Find the direction of \((-4,3)\).

1. \(\color{blue}{θ=30^\circ}\)
2. \(\color{blue}{|OA|=5}\)
3. \(\color{blue}{v⃗=3, 3\sqrt{3}}\)
4. \(\color{blue}{θ=143.13^\circ}\)