PSAT Math Practice Test Questions
Preparing for the PSAT Math test? Try these free PSAT Math Practice questions. Reviewing practice questions is the best way to brush up on your Math skills. Here, we walk you through solving 10 common PSAT Math practice problems covering the most important math concepts on the PSAT Math test.
These PSAT Math practice questions are designed to be similar to those found on the real PSAT Math test. They will assess your level of preparation and will give you a better idea of what to study for your exam.
The Absolute Best Book to Ace the PSAT Math Test
10 Sample PSAT Math Practice Questions
1- The area of a circle is \(64π\). What is the circumference of the circle?
A. \(8π\)
B. \(16π\)
C. \(32π\)
D. \(64π\)
2- Which of the following values for \(x\) and \(y\) satisfy the following system of equations?
\(x+4y=10\)
\(5x+10y=20\)
A. \(x=3,y=2\)
B. \(x=2,y=-3\)
C. \(x=-2,y=3\)
D. \(x=3,y=-2\)
3- If \(a ≠ 0\) and \(6b=5a\sqrt{3}\), then what is the value of \(\frac{2b \sqrt{3}}{4a}\) ?
A. \(\frac{5}{4}\)
B. \(\frac{5}{4}a\)
C. \(2a\)
D. \(2a\sqrt{3}\)
4- If a gas tank can hold 25 gallons, how many gallons does it contain when it is \( \frac{2}{5} \) full?
A. 50
B. 125
C. 62.5
D. 10
5- In the \(xy\)-plane, the point \((4,3)\) and \((3,2)\) are on line \(A\). Which of the following equations of lines is parallel to line \(A\)?
A. \(y = 3x\)
B. \(y = \frac{x}{2}\)
C. \(y = 2x\)
D. \(y = x\)
6- In the following graph, which of the data point is farthest from the line of best fit (not shown)?
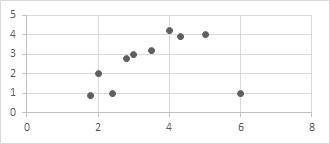
A. (6,1)
B. (5,4)
C. (3,3)
D. (2,2)
7- A football team won exactly \(80\%\) of the games it played during the last session. Which of the following could be the total number of games the team played last season?
A. 49
B. 35
C. 12
D. 32
8- If \(x\) is greater than 0 and less than 1, which of the following is true?
A. \(x<\sqrt {(x^2+1)}<\sqrt{(x^2 )}+1\)
B. \(x<\sqrt {(x^2 )}+1<\sqrt {(x^2+1)}\)
C. \((\sqrt {(x^{2} + 1)}< x <\sqrt {(x^{2} ) }+ 1\)
D. \(\sqrt {(x^{2} )}+1< \sqrt{(x^{2}+1) }< x\)
9- If \(x\) is directly proportional to the square of \(y\), and \(y=2\) when \(x=12\), then when \(x=75 y=\) ?
A. \(\frac{1}{5}\)
B. 1
C. 5
D. 12
10- Jack earns $616 for his first 44 hours of work in a week and is then paid 1.5 times his regular hourly rate for any additional hours. This week, Jack needs $826 to pay his rent, bills, and other expenses. How many hours must he work to make enough money this week?
A. 40
B. 48
C. 53
D. 54
Best PSAT Math Prep Resource for 2024
Answers:
1- B
Use the formula of areas of circles.
Area of a circle = \(πr^2→64 π=πr^2→64=r^2→r=8\)
The radius of the circle is 8. Now, use the circumference formula:
Circumference \(= 2πr = 2π (8) = 16π\)
2- C
\(x+4y=10\)
\(5x+10y=20\)
Multiply the top equation by -5 then,
\(-5x-20y=-50\)
\(5x+10y=20\)
Add two equations
\(-10y=-30→y=3 \) plug in the value of y into the first equation
\(x+4y=10→x+4(3)=10→x+12=10\)
Subtract 12 from both sides of the equation. Then:
\(x+12=10→x=-2\)
3- A
\(6b=5a\sqrt3→b= \frac{5a\sqrt3}{6}\)
\(Therefore:\)
\(\frac{2b\sqrt3}{4a}=\frac{2× \frac{5a\sqrt3}{6}×\sqrt3}{4a}=\frac{2×5a×3}{4×6a}=\frac{5}{4}\)
4- D
\( \frac{2}{5} ×25= \frac{50}{5} =10\)
5- D
The slop of line A is:
\(\frac{y_{2} – y_{1}}{x_{2} – x_{1}} = \frac{3-2}{4-3}=1 \)
Parallel lines have the same slope and only choice \(D (y=x)\) has slope of 1.
6- A
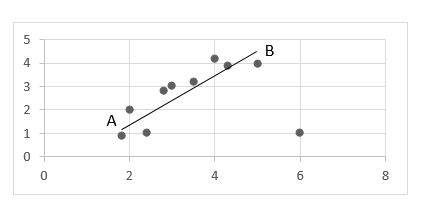
Line AB is the best fit line.
Then, point (6,1) is the farthest from line AB.
7- B
Choices \(A, C\) and \(D\) are incorrect because \(80\%\) of each of the numbers is a non-whole number.
\(49, 80 \% \ of \ 49 = 0.80×49=39.2\)
\(35, 80 \% \ of \ 35=0.80×35=28\)
\(12, 80 \% \ of \ 12=0.80×12=9.6\)
\(32, 80 \% \ of \ 32=0.80×32=25.6\)
8- A
Let \(x\) be equal to 0.5, then: \(x = 0.5\)
\(\sqrt{(x^2+1)}=\sqrt{(0.5^2+1)}=\sqrt{1.25}≈1.12\)
\(\sqrt{(x^2 )+1}=\sqrt{(0.5^2 )}+1=0.5+1=1.5\)
Then, option A is correct.
\(x<\sqrt{(x^2+1)}<\sqrt{(x^2 )}+1\)
9- C
\(x\) is directly proportional to the square of \(y\). Then:
\(x=cy^2\)
\(12=c(2)^2→12=4c→c=\frac{12}{4}=3\)
The relationship between \(x\) and y is:
\(x=3y^2\)
\(x=75\)
\(75= 3y^2 →y^2 = \frac{75}{3} = 25→y=5\)
10- D
The amount of money that jack earns for one hour:
\(\frac{$616}{44} =$14\)
Number of additional hours that he work to make enough money is:
\(\frac{$826-$616}{1.5×$14}=10\)Number of total hours is: \(44 + 10 = 54\)
College Entrance Tests
Looking for the best resource to help you succeed on the PSAT Math test?
The Best Books to Ace the PSAT Math Test
PSAT Math Practice Workbook 2024 The Most Comprehensive Review for the Math Section of the PSAT Test
Related to This Article
More math articles
- FREE 5th Grade STAAR Math Practice Test
- 10 Famous Math Problems and the History Behind Them
- How to Dividing Fractions by Whole Numbers in Recipes!
- Effective Strategies for Learning and Memorizing Math Formulas
- How to Write the Equation of a Cosine Graph?
- Number Navigators: How to Select Pairs with Targeted Sums and Differences
- 4th Grade MCAS Math Practice Test Questions
- How to Use Number Lines for Multiplication by a Negative Integer?
- A Comprehensive Guide to the Properties of Continuity in Functions
- How to Solve Trigonometric Equations?
What people say about "PSAT Math Practice Test Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.