Praxis Core Math FREE Sample Practice Questions

Preparing for the Praxis Core Math test? Looking for Praxis math practice questions to help you measure your exam readiness? To do your best on the Praxis Core Math test, you need to review and practice real Praxis Core Math questions.  There’s nothing like working on Praxis Core Math sample questions to hone your math skills and put you more at ease when taking the Praxis Core Math test. The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your Praxis Core Math test.

Check out our sample Praxis Core Math practice questions to find out what areas you need to practice more before taking the Praxis Core Math test!

Start preparing for the 2022 Praxis Core Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the Praxis Core Math Test

10 Sample Praxis Core Math Practice Questions

1- Which of the following has the same period and two times the amplitude of the graph
\(y = cos x\)?

A. \(y=cos 2x\)

B. \(y=cos (x+2)\)

C. \(y=4 cos⁡2x\)

D. \(y=2+2 cos x\)

E. \(y=4+cos x\)

2- Which of the following shows the numbers in increasing order?

A. \(\frac{2}{3},\frac{8}{11},\frac{5}{7},\frac{3}{4}\)

B. \(\frac{2}{3},\frac{5}{7},\frac{8}{11},\frac{3}{4}\)

C. \(\frac{5}{7},\frac{3}{4},\frac{8}{11},\frac{2}{3}\)

D. \(\frac{8}{11},\frac{3}{4},\frac{5}{7},\frac{2}{3}\)

E. None of the above

3- What’s the maximum ratio of the number of women to the number of men in each city?

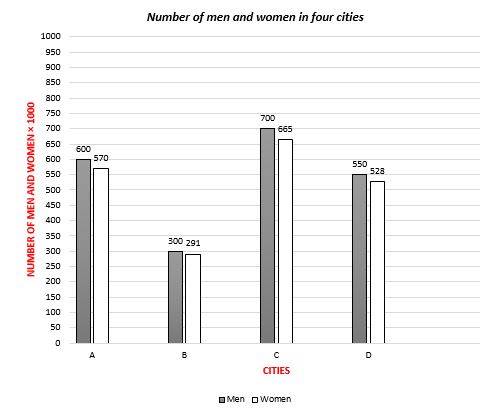
A. 0.98

B. 0.97

C. 0.96

D. 0.95

E. 0.94

4- What’s the ratio of the percentage of men in city A to the percentage of women in city C?

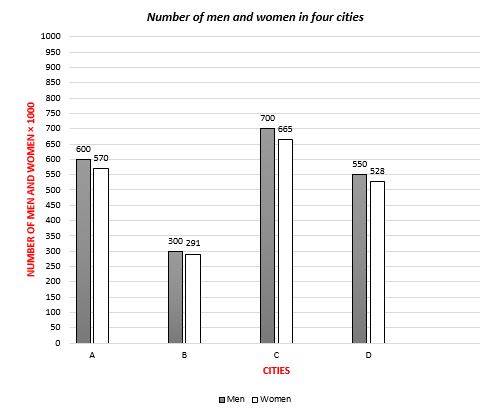
A. \(\frac{10}{9}\)

B. \(\frac{9}{10}\)

C. 1

D. \(\frac{19}{20}\)

E. \(\frac{20}{19}\)

5- How many women should be added to city D to change the ratio of women to men to 1.2?

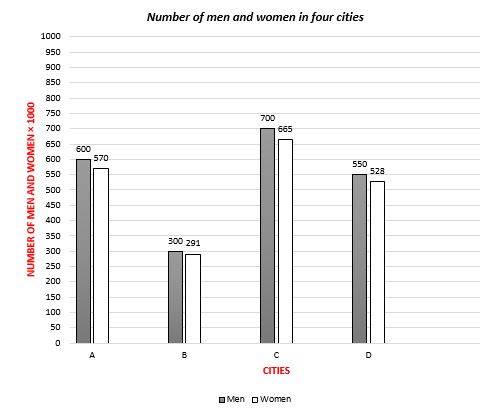
A. 130

B. 129

C. 132

D. 131

E. 133

6- In 1999, the average worker’s income increased by $2,000 per year starting from $24,000 annual salary. Which equation represents income greater than average? (I = income, \(x =\) number of years after 1999)

A. \(I>2000x+24000\)

B. \(I>–2000x+24000\)

C. \(I<–2000x+24000\)

D. \(I<2000x–24000\)

E. \(I<24,000x+24000\)

7- What are the values of mode and median in the following set of numbers?
1,2,2,5,4,4,3,3,3,1,1

A. Mode: 1, 2 Median: 2

B.  Mode: 1, 3 Median: 3

C. Mode: 2, 3 Median: 2

D. Mode: 1, 3 Median: 2.5

E. Mode: 3, Median: 3

8- If \(60\%\) of \(x\) equal to \(30\%\) of 20, then what is the value of \((x+5)^2\)?

A. 25.25

B. 26

C. 26.01

D. 2025

E. 225

9- In the \(xy\)-plane, the point (4,3) and (3,2) are on line A. Which of the following equations of lines is parallel to line A?

A. \(y=3x\)

B. \(y=10\)

C. \(y=\frac{x}{2}\)

D. \( y=2x\)

E. \(y=x\)

10- When point A (10, 3) is reflected over the y-axis to get point B, what are the coordinates of point B?

A. \((10, 3)\)

B. \((-10, -3)\)

C. \((-10, 3)\)

D. \((10, -3)\)

E. \((0, 3)\)

Best Praxis Core Math Prep Resource for 2022

Answers:

2- B
\(\frac{2}{3}≅0.67,\frac{8}{11}≅0.73,\frac{5}{7}≅0.71,\frac{3}{4}=0.75\)

3- B
ratio of A: \(\frac{570}{600}=0.95\)
ratio of B: \(\frac{291}{300}=0.97\)
ratio of C: \(\frac{665}{0.95}=0.95\)
ratio of D: \(\frac{528}{550} =0.96\)

4- E
First, find the percentage of men in city A and the percentage of women in city C.
Percentage of men in city A =\(\frac{600}{1170}\) and percentage of women in city C =\(\frac{665}{1365}\)
Find the ratio and simplify.
\(\frac{\frac{600}{1170}}{\frac{665}{1365}}=\frac{20}{19}\)

5- C
\(\frac{528+x}{550}==1.2→528+x=660→x=132\)

6- A
Let \(x\) be the number of years. Therefore, $2,000 per year equals \(2000x\).
starting from $24,000 annual salary means you should add that amount to \(2000x\).
Income more than that is:
\(I > 2000 x + 24000\)

7- B
We write the numbers in the order: 1, 1, 1, 2, 2, 3, 3, 3, 4, 4, 5
The mode of numbers is: 1 and 3, median is: 3

8- E
\(0.6x=(0.3)×20→x=10→(x+5)^2=(15)^2=225\)

9- E
The slop of line A is: m= \(\frac{y_2-y_1}{x_2-x_1}=\frac{3-2}{4-3}=1\)
Parallel lines have the same slope and only choice E \((y=x)\) has slope of 1.

10- C
When points are reflected over \(y\)-axis, the value of \(y\) in the coordinates doesn’t change and the sign of \(x\) changes. Therefore, the coordinates of point B is \((-10,3)\).

Looking for the best resource to help you succeed on the Praxis Core Math test?

The Best Books to Ace the Praxis Core Math Test