ISEE Upper-Level Math FREE Sample Practice Questions
Preparing your student for the ISEE Upper-Level Math test? To help students do their best on the ISEE Upper-Level Math test, they need to review and practice real ISEE Upper-Level Math questions. There’s nothing like working on ISEE Upper-Level Math sample questions to hone your students’ math skills and put them more at ease when taking the ISEE Upper-Level Math test. The sample math questions you’ll find here are brief samples designed to give students the insights they need to be as prepared as possible for their ISEE Upper-Level Math test.
Check out our sample ISEE Upper-Level Math practice questions to find out what areas your students need to practice more before taking the ISEE Upper-Level Math test!
Help your students start preparing for the 2022 ISEE Upper-Level Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the ISEE Upper Level Math Test
10 Sample ISEE Upper Level Math Practice Questions
1- Use the following table to answer the question below.
This table shows the data Daniel collected while watching birds for one week. How many raptors did Daniel see on Monday?
A. 10
B. 11
C. 12
D. 13
2- A floppy disk shows 937,036 bytes free and 739,352 bytes used. If you delete a file of size 652,159 bytes and create a new file of size 599,986 bytes, how many free bytes will the floppy disk have?
A. 687,179
B. 791,525
C. 884,867
D. 989,209
3- 5 days 19 hours 35 minutes \(– 3\) days 12 hours 22 minutes \(=\)?
A. 3 days 10 hours 13 minutes
B. 2 days 7 hours 13 minutes
C. 3 days 10 hours 13 minutes
D. 2 days 7 hours 23 minutes
4- The base of a right triangle is 2 feet, and the interior angles are \(45-45-90\). What is its area?
A. 2 foot squared
B. 4 foot squared
C. 3.5 foot squared
D. 5.5 foot squared
5- Increased by \(50\%\), the numbers 84 becomes:
A. 42
B. 100
C. 126
D. 130
6- Which equation represents the statement twice the difference between 6 times h and 3 gives 30.
A. \(\frac{6h + 3}{2}= 30\)
B. \(6(2h + 3) = 30\)
C. \(2(6h – 3) = 30\)
D. \(3\frac{6h}{2}= 30\)
7- A circle is inscribed in a square, as shown below.
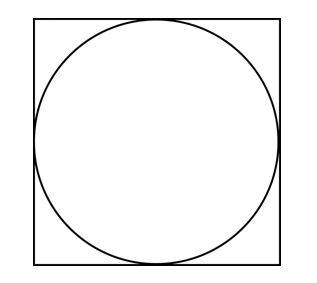
The area of the circle is \(16π\)cm\(^2\). What is the area of the square?
A. \(8 \space \)cm\(^2\)
B. \(16 \space \)cm\(^2\)
C. \(48 \space \)cm\(^2\)
D. \(64 \space \)cm\(^2\)
8- If \(10 + x^{\frac{1}{2}} = 14\), then what is the value of \(15 × x\)?
A. 15
B. 60
C. 120
D. 240
9- Triangle ABC is graphed on a coordinate grid with vertices at A \((-3, -2)\), B \((-1, 4)\) and C\( (7, 9)\). Triangle ABC is reflected over \(x\) axes to create triangle A’B’C’.
Which order pair represents the coordinate of C’?
A. \((7, 9)\)
B. \((-7, -9)\)
C. \((-7, 9)\)
D. \((7, -9)\)
10- Which set of ordered pairs represents\( y\) as a function of \(x\)?
A. \({(3, -2), (3, 7), (9, -8), (4, -7)}\)
B. \({(4, 2), (3, -9), (5, 8), (4, 7)}\)
C. \({(9, 12), (5, 7), (6, 11), (5, 18)}\)
D.\( {(6, 1), (3, 1), (0, 5), (4, 5)}\)
Best ISEE Upper Level Math Prep Resource for 2024
Answers:
1- A
\(\frac{x+9+14+12+5}{5}=10 → x + 40 = 50 → x = 50 – 40 = 10\)
2- D
The difference of the file added, and the file deleted is:
\( 652,159 – 599,986 = 52,173\)
\(937,036 + 52,173 = 989,209\)
3- B
5 days 19 hours 35 minutes \(– 3\) days 12 hours 22 minutes \(=\) 2 days 7 hours 13 minutes
4- A
Formula of triangle area =\( \frac{1}{2} (base × height)\)
Since the angles are \(45-45-90\), then this is an isosceles triangle, meaning that the base and height of the triangle are equal.
Triangle area = \(\frac{1}{2}\)
(base × height) = \(\frac{1}{2} (2 × 2) = 2\)
5- C
\(50\%\) of \(84 = 42\)
\(84 + 42= 126\)
6- C
\(2(6h – 3) = 30\)
7- D
The area of the circle is \(16π\) cm\(^2\), then, its diameter is 8cm.
\(area \space of \space a \space circle \space = πr^2=16π→r^2=16→r=4\)
Radius of the circle is 4 and diameter is twice of it, 8.
One side of the square equals the diameter of the circle. Then:
\( Area \space of \space square \space = side×side=8×8=64\)
8- D
\(x^\frac{1}{2}\) equals to the root of \(x\). Then:
\(10+x^\frac{1}{2}=14→10+\sqrt x=14→\sqrt x=4→x=16\)
\(x = 16\) and \(15 × x\) equals: \(15 × 16 = 240\)
9- D
When a point is reflected over \(x\) axes, the \((y)\) coordinate of that point changes to \((-y)\) while its \(x\) coordinate remains the same.
\(C (7, 9) → C’ (7, -9)\)
10- D
A set of ordered pairs represents \(y\) as a function of \(x\) if:
\( x_1=x_2→y_1=y_2 \)
In choice A: \((3, -2)\) and \((3, 7)\) are ordered pairs with same \(x \)and different \(y\), therefore \(y\) isn’t a function of \(x\).
In choice B:\( (4, 2)\) and\( (4, 7) \)are ordered pairs with same \(x \)and different \(y\), therefore\( y\) isn’t a function of \(x\).
In choice C: \((5, 7)\) and\( (5, 18)\) are ordered pairs with same\( x\) and different\( y\), therefore \(y\) isn’t a function of \(x\).
The Best Books to Ace the ISEE Upper Level Math Test
ISEE Upper Level Math Study Guide Step-By-Step Guide to Preparing for the ISEE Upper Level Math Test
Related to This Article
More math articles
- FREE 4th Grade STAAR Math Practice Test
- A Comprehensive Collection of FREE SAT Math Practice Tests
- Identify 3–Dimensional Figures
- 4th Grade Wisconsin Forward Math Worksheets: FREE & Printable
- Top 10 3rd Grade FSA Math Practice Questions
- What Skills Do I Need for the ALEKS Math Test?
- 3rd Grade PEAKS Math Worksheets: FREE & Printable
- How to Calculate the Volume of a Truncated Cone: Step-by-Step Guide
- The Ultimate GRE Math Course: The Only Course You Need for Success
- Top 10 4th Grade Georgia Milestones Assessment System Math Practice Questions
What people say about "ISEE Upper-Level Math FREE Sample Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.