10 Most Common ISEE Upper-Level Math Questions
Preparing for the ISEE Upper-Level Math test? Want a preview of the most common mathematics questions on the ISEE Upper-Level Math test? If so, then you are in the right place.
The mathematics section of ISEE Upper Level can be a challenging area for many test-takers, but with enough patience, it can be easy and even enjoyable!
Preparing for the ISEE Upper-Level Math test can be a nerve-wracking experience. Learning more about what you’re going to see when you take the ISEE Upper Level can help to reduce those pre-test jitters. Here’s your chance to review the 10 most common ISEE Upper-Level Math questions to help you know what to expect and what to practice most. Try these 10 most common ISEE Upper-Level Math questions to hone your mathematical skills and to see if your math skills are up to date on what’s being asked on the exam or if you still need more practice.
Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the ISEE Upper Level Math Test
10 Sample ISEE Upper Level Math Practice Questions
1- Emily and Daniel have taken the same number of photos on their school trip. Emily has taken 5 times as many photos as Claire and Daniel has taken 16 more photos than Claire. How many photos has Claire taken?
A. 4
B. 6
C. 8
D. 10
2- Emily lives 5 \(\frac{1}{4}\) miles from where she works. When traveling to work, she walks to a bus stop \(\frac{1}{3}\) of the way to catch a bus. How many miles away from her house is the bus stop?
A. \(4\frac{1}{3}\) miles
B. \(4\frac{3}{4}\) miles
C. \(2\frac{3}{4}\) miles
D. \(1\frac{3}{4}\) miles
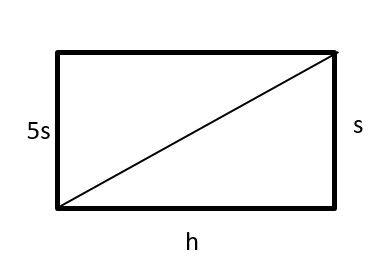
3- Use the diagram below to answer the question.
Given the lengths of the base and diagonal of the rectangle above, what is the length of height h, in terms of s?
A. 2s \(\sqrt{6}\)
B. s \(\sqrt{7}\)
C. 5s
D. 5s\(^2\)
4-
There are also purple marbles in the bag. Which of the following can NOT be the probability of randomly selecting a purple marble from the bag?
A. \(\frac{1}{10}\)
B. \(\frac{1}{4}\)
C. \(\frac{2}{5}\)
D. \(\frac{7}{15}\)
5- A square measures 6 inches on one side. By how much will the area be increased if its length is increased by 5 inches and its width decreased by 3 inches.
A. 1 sq decreased
B. 3 sq decreased
C. 6 sq decreased
D. 9 sq decreased
6- If a box contains red and blue balls in the ratio of \(2 : 3\) red to blue, how many red balls are there if 90 blue balls are in the box?
A. 40
B. 60
C. 80
D. 30
7- How many \(3 × 3\) squares can fit inside a rectangle with a height of 54 and width of 12?
A. 72
B. 52
C. 62
D. 42
8- David makes a weekly salary of $220 plus \(8\%\) commission on his sales. What will his income be for a week in which he makes sales totaling $1100?
A. $328
B. $318
C. $308
D. $298
9- \(4x^2y^3 + 5x^3y^5 – (5x^2y^3 – 2x^3y^5) = \)
A. \(–x^2y^3\)
B. \(6x^2y^3 – x^3y^5\)
C. \(7x^2y^3\)
D. \(7x^3y^5 – x^2y^3\)
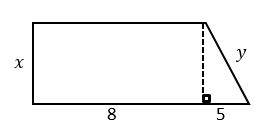
10- If the area of trapezoid is 126 cm, what is the perimeter of the trapezoid?
Best ISEE Upper Level Math Prep Resource for 2024
Answers:
1- A
Emily = Daniel
Emily = 5 Claire
Daniel = \(16 +\) Claire
Emily = Daniel → Emily = \(16 +\) Claire
Emily = 5 Claire → 5 Claire = \(16 +\) Claire → 5 Claire \(–\) Claire = 16
4 Claire = 16
Claire = 4
2- D
\(\frac{1}{3}\) of the distance is \(5\frac{1}{4}\) miles. Then:
\(\frac{1}{3} × 5 \frac{1}{4} = \frac{1}{3} × \frac{21}{4}= \frac{21}{12}\)
Converting \(\frac{21}{12}\) to a mixed number gives:
\(\frac{21}{12}= 1\frac{9}{12}=1\frac{3}{4}\)
3- A
Use Pythagorean theorem:
\(a^2+b^2=c^2→s^2+h^2=(5s)^2→s^2+h^2=25s^2\)
Subtracting (s^2) from both sides gives: \( h^2=24s^2\)
Square roots of both sides: \(h=\sqrt{24s^2}=\sqrt{4×6×s^2 } =\sqrt 4 × \sqrt6 × \sqrt{s^2 }=2 × s × \sqrt6 = 2s\sqrt6\)
4- D
Let \(x\) be the number of purple marbles. Let’s review the choices provided:
A. \(\frac{1}{10}\), if the probability of choosing a purple marble is one out of ten, then:
\(Probability=\frac{number \space of \space desired \space outcomes}{number \space of \space total \space outcomes}=\frac{x}{20+30+40+x}=\frac{1}{10}\)
Use cross multiplication and solve for x. \(10x=90+x→9x=90→x=9\)
Since the number of purple marbles can be 9, then, the choice is the probability of randomly selecting a purple marble from the bag.
Use the same method for other choices.
B. \(\frac{1}{4}\)
\(\frac{x}{20+30+40+x}=\frac{1}{4}→4x=90+x→3x=90→x=30\)
C. \(\frac{2}{5}\)
\(\frac{x}{20+30+40+x}=\frac{2}{5}→5x=180+2x→3x=180→x=60\)
D. \(\frac{7}{15}\)
\(\frac{x}{20+30+40+x}=\frac{7}{15}→15x=630+7x→8x=630→x=78.75\)
The number of purple marbles cannot be a decimal.
5- B
The area of the square is 36 square inches.
\(Area of square=side×side=6×6=36\)
The length of the square is increased by 5 inches and its width decreased by 3 inches. Then, its area equals:
Area of \(rectangle=width×length=11×3=33\)
The area of the square will be decreased by 3 square inches.
\(36-33=3\)
6- B
Write a proportion and solve.
\(\frac{2}{3}=\frac{x}{90}\)
Use cross multiplication:
\(3x=180→x=60\)
7- A
Number of squares equal to: \(\frac{54×12}{3×3} = 18 × 4 = 72\)
8- C
David’s weekly salary is $220 plus \(8\%\) of $1,100. Then:
\(8\% \space of \space 1,100=0.08 × 1,100 = 88\)
\(220+88=308\)
9- D
\(4x^2y^3 + 5x^3y^5 – (5x^2y^3 – 2x^3y^5) = 4x^2y^3 + 5x^3y^5 – 5x^2y^3 + 2x^3y^5 = – x^2y^3 + 7 x^3y^5\)
10- 13
The area of the trapezoid is:
\(Area=\frac{1}{2}h(b_1+b_2 )=\frac{1}{2}(x)(13+8)=126\)
\(→10.5x=126→x=12\)
\(y=\sqrt{5^2 +12^2 } = \sqrt{25+144} = \sqrt{169} = 13\)
Looking for the best resource to help you succeed on the ISEE Upper Level Math test?
The Best Books to Ace the ISEE Upper Level Math Test
ISEE Upper Level Math Study Guide Step-By-Step Guide to Preparing for the ISEE Upper Level Math Test
Related to This Article
More math articles
- How to Determine the Classification of a System of Equations?
- Accuplacer Math Formulas
- Full-Length PSAT 10 Math Practice Test
- Narrowing Down to One Variable with the Help of Implicit Differentiation
- Table Tales: How to Finding the Rule in Word Problems
- How to Prepare for the FSA Math Test?
- Using Properties to Convert Traditional and Metric Units
- How to Calculate the Volume of Cubes and Prisms
- 5th Grade AZMerit Math Worksheets: FREE & Printable
- How to Find the Integral of Radicals
What people say about "10 Most Common ISEE Upper-Level Math Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.