TSI Math FREE Sample Practice Questions
Preparing for the TSI Math test? To do your best on the TSI Math test, you need to review and practice real TSI Math questions. There’s nothing like working on TSI Math sample questions to hone your math skills and put you more at ease when taking the TSI Math test. The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your TSI Math test.
Check out our sample TSI Math practice questions to find out what areas you need to practice more before taking the TSI Math test!
Start preparing for the 2026 TSI Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.
The Absolute Best Book to Ace the TSI Math Test
B. \(-6\)
C. \(5\)
D. \(-5\)
8- If \(log_2x = 5\), then \(x =\) ?
A. \(2^{10}\)
B. \(\frac{5}{2}\)
C. \(2^{6}\)
D. \(32\)
9- What’s the reciprocal of \(\frac{x^3}{16}\) ?
A. \(\frac{16}{x^3}-1\)
B. \(\frac{48}{x^3}\)
C. \(\frac{16}{x^3}+1\)
D. \(\frac{16}{x^3}\)
10- Find the inverse function for \(ln (2x + 1)\)
A. \(\frac{1}{2}(e^{x }– 1)\)
B. \((e^{x }+ 1)\)
C. \(\frac{1}{2}(e^{x }+ 1)\)
D. \((e^{x }– 1)\)
Best TSI Math Prep Resource for 2026
Answers:
1- C
METHOD ONE
\(log_4(x+2) – log_4(x-2) = 1\)
Add\(\space log_4(x-2)\)to both sides
\(log_4(x+2) – log_4(x-2)+ log_4(x-2)= 1 + log_4(x-2)\)
\(log_4(x+2) = 1 + log_4(x-2)\)
Apply logarithm rule:
\(a = log_b(b^a) ⇒ 1 = log_4(4^1) = log_4(4)\)
\(then: log_4(x+2) = log_4(4) + log_4(x-2)\)
\(Logarithm \space rule: log_c(a) + log_c(b) = log_c(ab)\)
\(then: log_4(4) + log_4(x-2) = log_4(4(x-2))\)
\(log_4(x+2) = log_4(4(x-2))\)
When the logs have the same base:
\(log_b(f(x)) = log_b(g(x)) ⇒ f(x) = g(x) (x+2) = 4(x-2)\)
\(x = \frac{10}{3}\)
METHOD TWO
We know that:
\(log_ab-log_ac=log_a\frac{b}{c}\space and \space log_ab=c⇒b=a^c\)
Then: \(log_4(x+2)- log_4(x-2)=log_4\frac{(x + 2)}{(x – 2)}=1⇒\frac{(x + 2)}{(x-2)}=4^1=4⇒x+2=4(x-2)⇒x+2=4x-8⇒4x-x=8+2→3x=10⇒x=\frac{10}{3}\)
2- B
\(e^{(5x + 1 )}= 10\)
If\( \space f(x) = g(x)\), then \(\space ln(f(x)) = ln(g(x))\)
\(ln(e^{(5x + 1 )})= ln(10)\)
Apply logarithm rule:
\(log_a(x^b) = b log_a(x)\)
\(ln(e^{(5x + 1 )})= (5x + 1)ln(e)\)
\((5x + 1)ln(e) = ln(10)\)
\((5x + 1)ln(e) = (5x + 1)\)
\((5x + 1) = ln(10) \)
\( ⇒x = \frac{ln(10) – 1}{5}\) For additional educational resources, . For additional educational resources, visit the U.S. Department of Education website.
3- C
\(f(x) = x –\frac{5}{3}⇒ y = x – \frac{5}{3}⇒ y+ \frac{5}{3}=x\)
\(f^{-1 }= x+ \frac{5}{3}\)
\(f ^{–1}(5) = 5 +\frac{5}{3}=\frac{20}{3}\) For additional educational resources, .
4- C
\(cos\)\( 30^\circ = \frac{\sqrt 3}{2}\) For additional educational resources, .
5- C For additional educational resources, .
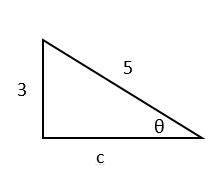
sin\(θ=\frac{3}{5}\)⇒ we have following triangle, then:
\(c=\sqrt {(5^2-3^2 )}=\sqrt{(25-9)}=\sqrt 16=4\)
cos\(θ=\frac{4}{5}\) For additional educational resources, .
6- B
\(-2x- y = -9\)
\(5x-2y= 18\)
⇒ Multiplication \((–2)\) in first equation
\(4x +2y =18\)
\(5x-2y= 18\)
Add two equations together ⇒\( 9x =36 ⇒ x= 4\) then: \(y = 1\) For additional educational resources, .
7- C
\(|9 – (12 ÷ | 2 – 5 |)| = |(9-(12÷|-3|))|=|9-(12÷3)|=|9-4|=|5|=5\) For additional educational resources, .
8- D
METHOD ONE
\(log_2x = 5\)
Apply logarithm rule:\(a = log_b(b^a)\)
\(5 = log_2(2^5) = log_2(32)\)
\(log_2x = log_2(32)\)
When the logs have the same base: \(log_b(f(x)) = log_b(g(x))⇒ f(x) = g(x)\)
then: \(x = 32\)
METHOD TWO
We know that:
\(log_ab=c⇒b=a^c\)
\(log_2x=5⇒x=2^5=32\) For additional educational resources, .
9- D
\(\frac{x^3}{16}\)
⇒ reciprocal is : \(\frac{16}{x^3}\) For additional educational resources, .
10- A
\(f(x) = ln (2x + 1)\)
\(y = ln (2x + 1)\)
Change variables \( x\) and \(y: x = ln (2y + 1)\)
solve: \(x = ln (2y + 1)\)
\(y = \frac{e^{x}-1}{2}=\frac{1}{2}(e^{x} – 1)\) For additional educational resources, .
Looking for the best resource to help you succeed on the TSI Math test? For additional educational resources, .
The Best Books to Ace the TSI Math Test
More from Effortless Math for TSI Test …
Are you looking for prep books that will guarantee you a high score on the TSI math test?
Top 10 TSI Math Prep Books (Our 2021 Favorite Picks) helps you find the best book for you
Worried about TSI exam day?
TSI Math-Test Day Tips briefly provides you with important tips for the exam day.
Do you know the formulas for the TSI math test?
If you have not thought about this yet, do not worry! We provide you with a complete list of formulas: TSI Math Formulas.
The Perfect Prep Books for the TSI Math Test
Have any questions about the TSI Test?
Write your questions about the TSI or any other topics below and we’ll reply!
Related to This Article
More math articles
- A Comprehensive Collection of Free GED Math Practice Tests
- Top 10 Tips to ACE the ISEE Math Test
- Top 10 7th Grade FSA Math Practice Questions
- How to Write an Exponential Function: Word Problems
- 8th Grade NYSE Math Worksheets: FREE & Printable
- The Ultimate SIFT Math Formula Cheat Sheet
- The Ultimate 7th Grade Scantron Math Course (+FREE Worksheets)
- Top 10 Tips to Overcome CLEP College Math Anxiety
- What Kind of Math Is on the AFOQT Test?
- Effective Strategies for Learning and Memorizing Math Formulas
What people say about "TSI Math FREE Sample Practice Questions - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.