Mastering Exponential Growth And Decay: A Comprehensive Guide

Exponential growth and decay are mathematical models used to describe how quantities change over time at a constant relative rate. They are characterized by their rapid initial change and the fact that the rate of change (growth or decay) remains constant throughout the process. These concepts have wide applications in various scientific, economic, and real-world scenarios.

Exponential Growth:

Exponential growth occurs when a quantity increases at a constant relative rate over time. In other words, the rate of growth is directly proportional to the current value of the quantity. The general form of an exponential growth equation is: \(A(t) = A_0 \cdot e^{rt},\) where:

• \(A(t)\) is the quantity at time \(t\).
• \(A_0\) is the initial quantity at \(t = 0\).
• \(r\) is the growth rate, often expressed as a decimal.
• \(e\) is the base of the natural logarithm, approximately equal to \(2.71828\). The growth rate \(r\) determines how quickly the quantity increases. If \(r > 0\), the quantity is growing, and if \(r < 0\), it’s decaying. Key characteristics of exponential growth:
• Rapid increase over time, especially as \(t\) becomes large.
• The growth rate remains constant.
• There is no upper limit to the growth unless constrained by external factors. Examples of exponential growth include population growth (in idealized conditions), compound interest on investments, and the spread of infectious diseases in a susceptible population.

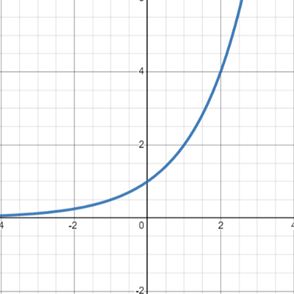
Exponential Decay:

Exponential decay, on the other hand, describes the decrease of a quantity at a constant relative rate over time. The general form of an exponential decay equation is similar to the growth equation but with a negative exponent: \(A(t) = A_0 \cdot e^{-rt},\) where the same variables apply as in the growth equation. Key characteristics of exponential decay:

• Rapid initial decrease followed by a slower decline.
• The decay rate \((-r)\) remains constant.
• There is no lower limit to the decay unless constrained by external factors. Examples of exponential decay include the decay of radioactive isotopes and the decrease in the number of bacteria after the introduction of antibiotics.

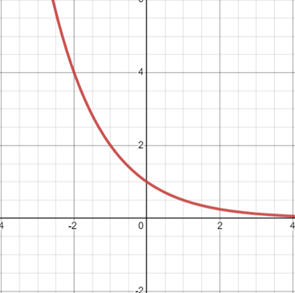
Half-Life:

The concept of half-life is closely related to exponential decay. The half-life \((t_{\text{1/2}})\) is the time it takes for half of the initial quantity to decay. It can be calculated using the exponential decay formula:

\(t_{\text{1/2}} = \frac{\ln(2)}{r},\)

where \(\ln(2)\) is the natural logarithm of \(2\), and \(r\) is the decay rate.

Half-life is a useful parameter in fields like nuclear physics (for radioactive decay) and pharmacology (for drug elimination from the body).

Graphical Representation:
When you graph exponential growth and decay, you’ll notice distinctive curves:

• Exponential growth results in an upward-sloping curve that becomes steeper as time progresses.
• Exponential decay results in a downward-sloping curve that becomes less steep as time progresses. The shape of these curves is determined by the growth or decay rate \((r)\).