FREE ISEE Upper Level Math Practice Test

Welcome to our FREE ISEE Upper-Level Math practice test, with answer key and answer explanations. This practice test’s realistic format and high-quality practice questions can help your students succeed on the ISEE Upper-Level Math test. Not only does the test closely match what your students will see on the real ISEE Upper Level, but it also comes with detailed answer explanations.

For this practice test, we’ve selected 20 real questions from past exams for your students’ ISEE Upper-Level Practice test. Test takers will have the chance to try out the most common ISEE Upper-Level Math questions. For every question, there is an in-depth explanation of how to solve the question and how to avoid mistakes next time.

Use our free ISEE Upper-Level Math practice tests and study resources (updated for 2022) to help your students ace the ISEE Upper-Level Math test! Make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions students need to practice.

The Absolute Best Book to Ace the ISEE Upper Level Math Test

10 Sample ISEE Upper Level Math Practice Questions

1- How is this number written in scientific notation?
0.00002389

A. \(2.389 × 10^{-5}\)

B. \(23.89 × 10^6\)

C. \(0.2389 × 10^{-4}\)

D. \(2389 × 10^{-8}\)

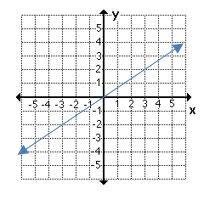
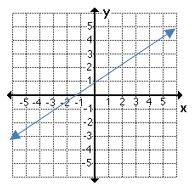
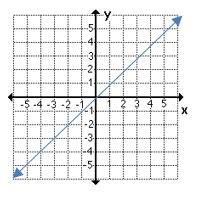
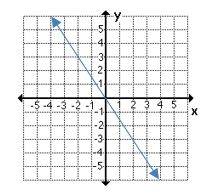
2- Which graph shows a non-proportional linear relationship between \(x\) and \(y\)?

A.

B.

C.

D.

3- The rectangle on the coordinate grid is translated 5 units down and 4 units to the left.

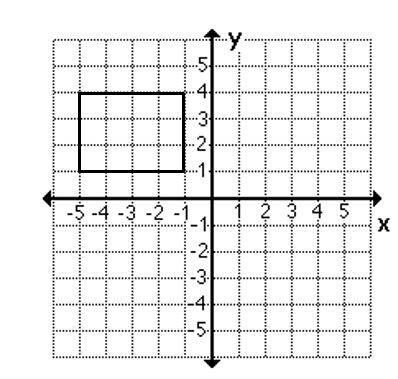
Which of the following describes this transformation?

A. \((x,y) ⇒ (x-4,y+5)\)

B. \( (x,y) ⇒ (x-4,y-5)\)

C. \( (x,y) ⇒ (x+4,y+5)\)

D. \( (x,y) ⇒ (x+4,y-5)\)

4- A girl 160 cm tall, stands 360 cm from a lamp post at night. Her shadow from the light is 90 cm long. How high is the lamp post?

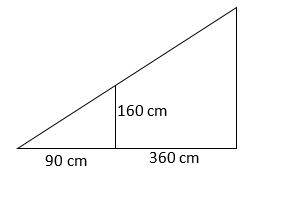
A. 240

B. 400

C. 600

D. 800

5- Which value of \(x\) makes the following inequality true?
\(\frac{3}{22}≤ x < 19%\)

A. 0.13

B. \(\frac{5}{36}\)

C. \(\sqrt{0.044}\)

D. 0.124

6- The ratio of boys to girls in a school is 5:3. If there are 640 students in a school, how many boys are in the school?

A. 240

B. 360

C. 400

D. 540

7- The width of a box is one-third of its length. The height of the box is one-third of its width. If the length of the box is 27 cm, what is the volume of the box?

A. 81 cm\(^3\)

B. 162 cm\(^3\)

C. 243 cm\(^3\)

D. 729 cm\(^3\)

8- The drivers at G & G trucking must report the mileage on their trucks each week. The mileage reading of Ed’s vehicle was 40,907 at the beginning of one week, and 41,053 at the end of the same week. What was the total number of miles driven by Ed that week?

A. 46 miles

B. 145 miles

C. 146 miles

D. 1046 miles

9- Which equation represents the statement Three plus the sum of the squares of \(w\) and \(x\) is 32.

A. 42

B. \(3(w^2 + x) = 32\)

C. 126

D. 130

10- What is the solution of the following system of equations?
\(-2x- y = -9 \)
\(5x-2y= 18\)

A. \((-1, 2)\)

B. \((4, 1)\)

C. \((1, 4)\)

D. \((4, -2)\)

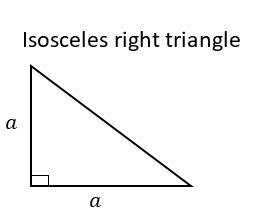
11- What is the area of an isosceles right triangle that has one leg that measures 6 cm?

A. 18 cm

B. 36 cm

C. 6 \(\sqrt{2}\) cm

D. 72 cm

12- Which of the following is a factor of both \(x^2 – 2x – 8\) and \(x^2 – 6x + 8\)?

A. \((x – 4)\)

B. \((x + 4)\)

C. \((x – 2)\)

D. \((x + 2)\)

13- \(\frac{1}{6b^2} + \frac{1}{6b} = \frac{1}{b^2}\)

A. \(-\frac{16}{15}\)

B. 5

C. \(-\frac{15}{16}\)

D. 8

14- \(\frac{|3+x|}{7}≤ 5, \space then \space x = ?\)

A. \(–38 ≤ x ≤ 35\)

B. \(–38 ≤ x ≤ 32\)

C. \(–32 ≤ x ≤ 38\)

D. \(–32 ≤ x ≤ 32\)

15- The cost, in thousand of dollars, of producing \(x\) thousands of textbooks is \(C (x) = x^2 + 10x + 30\). The revenue, also in thousands of dollars, is \(R(x) = 4x\). find the profit or loss if 3,000 textbooks are produced. (profit \(=\) revenue \(–\) cost)

A. $21,000 loss

B. $57,000 profit

C. $3,000 profit

D. $240 loss

16- Ella (E) is 4 years older than her friend Ava (A) who is 3 years younger than her sister Sofia (S). If E, A, and S denote their ages, which one of the following represents the given information?

A. \(E=A+4\)
\(S=A-3\)

B. \(E=A+4\)
\(A=S+3\)

C. \(A=E+4\)
\(S=A-3\)

D. \(E=A+4\)
\(A=S-3\)

17- Which is the longest time?

A. 23 hours

B. 1520 minutes

C. 2 days

D. 4200 seconds

18- Write 523 in expanded form, using exponents.

A. \((5 × 10^3) + (2 × 10^2) + (3 × 10)\)

B. \((5 × 10^2) + (2 × 10^1) – 5\)

C. \( (5 × 10^2) + (2 × 10^1) + 3\)

D. \((5 × 10^1) + (2 × 10^2) + 3\)

19- A company pays its writer $4 for every 400 words written. How much will a writer earn for an article with 960 words?

A. $11

B. $5.6

C. $9.6

D. $8.7

20- A circular logo is enlarged to fit the lid of a jar. The new diameter is \(60\%\) larger than the original. By what percentage has the area of the logo increased?

A. \(40\%\)

B. \(30\%\)

C. \(60\%\)

D. \(20\%\)

Best ISEE Upper Level Math Prep Resource for 2024

Answers:

2- B
A linear equation is a relationship between two variables, \(x\) and \(y\), and can be written in the form of \(y = mx + b\).
A non-proportional linear relationship takes on the form \(y=mx + b\), where \(b ≠ 0\) and its graph is a line that does not cross through the origin.

3- B
Translated 5 units down and 4 units to the left means: \((x.y) ⇒ (x-4,y-5)\)

4- D
Write the proportion and solve for the missing side.
\(\frac{Smaller \space triangle \space height}{Smaller \space triangle \space base}=\frac{Bigger \space triangle \space height}{Bigger \space triangle \space base} ⇒\frac{90 \space cm}{160 \space cm}=\frac{90 + 360 \space cm}{x} ⇒ x = 800 \space\) cm

5- B
\(\frac{3}{22} = 0.136 \)and \(19\% = 0.19\) therefore \(x\) should be between 0.136 and 0.19
Choice B. \(5/36 = 0.138\) is between 0.136 and 0.19

6- A
The ratio of boys to girls is 2:3. Therefore, there are 2 boys out of 5 students. To find the answer, first divide the total number of students by 5, then multiply the result by 2.
\(600 ÷ 5 = 120 ⇒ 120 × 2 = 240\)

7- D
If the length of the box is 27, then the width of the box is one-third of it, 9, and the height of the box is 3 (one-third of the width). The volume of the box is:
V = lwh = \((27) (9) (3) = 729\)

8- C
To find the total number of miles driven by Ed that week, you only need to subtract 40,907 from 41,053.
\(41,053-40,907=146\)

9- B
\(3(w^2 + x) = 32\)

10- B
\(-2x- y = -9\)
\(5x-2y= 18\)
⇒ Multiplication \((–2)\) in first equation ⇒
\(4x +2y =18\)
\(5x-2y= 18 \)
Add two equations together \(⇒ 9x =36 ⇒ x= 4\) then: \(y = 1\)

11- A
First, draw an isosceles triangle. Remember that two sides of the triangle are equal.
Let’s put a for the legs. Then:
\(a=6⇒\) area of the triangle is = \(\frac{1}{2}(6×6)=\frac{36}{2} = 18 \)cm\(^2\)

12- A
Factor each trinomial \(x^2 – 2x – 8\) and \(x^2 – 6x + 8\)
\(x^2 – 2x – 8 ⇒ (x – 4)(x + 2) \)
\(x^2 – 6x + 8 ⇒ (x – 2)(x – 4)\)

13- B
Subtract \(\frac{1}{6b}\) and \(\frac{1}{b^2}\) from both sides of the equation. Then:
\(\frac{1}{6b^2}+\frac{1}{6b}=\frac{1}{b^2}→\frac{1}{6b^2}-\frac{1}{b^2}=-\frac{1}{6b}\)
Multiply both the numerator and denominator of the fraction \(\frac{1}{b^2}\) by 6. Then:
\(\frac{1}{6b^2}-\frac{6}{6b^2}=-\frac{1}{6b}\)
Simplify the first side of the equation:
\(-\frac{5}{6b^2}=-\frac{1}{6b}\)
Use cross multiplication method: \( 30b=6b^2→30=6b→b=5\)

14- B
First, multiply both sides of the inequality by 7. Then:
\(\frac{|3+x|}{7}≤ 5→|3+x|≤35\)
Since \(3+x\) can be positive or negative, then:
\(3+x≤35\) or \(3+x≥-35\)
Then:
\(x≤32\) or \(x≥-38\)
Choice B is correct.

15- D
Plug in the value of \(x=30\) into both equations. Then:
\(C(x) = x^2+2x=(30)^2+2(30)=900+60=960\)
\(R(x)=40x=40×30=1,200 \)
\(1,200 – 960 = 240\)

16- D
\(E = 4 + A\)
\(A = S – 3\)

17- C
\(23\) hours \(= 82,800\) seconds
\(1520\) minutes \(= 91,200\) seconds
\(2\) days\( = 48\) hours \(= 172,800\) seconds
4200 seconds

18- C
Let’s review the choices provided:
A. \((5 × 103) + (2 × 102) + (3 × 10) = 5,000 + 200 + 30 = 5,230\)
B. \((5 × 102) + (2 × 101) – 5 = 500 + 20 – 5 = 515\)
C. \((5 × 102) + (2 × 101) + 3 = 500 + 20 + 3 = 523\)
D. \((5 × 101) + (2 × 102) + 3 = 50 + 20 + 3 = 73\)
Only choice C equals to 523.

19- C
\(\frac{4}{400}=\frac{x}{960}\)
\(x = \frac{4 × 960}{400} = 9.6\)

20- B
The area of a circle equals:
\(A=πr^2\)
The new diameter is \(30\%\) larger than the original then the new radius is also \(30\%\) larger than the original.
\(30\%\) larger than r is \(1.3r\).
Then, the area of the larger circle is:
\(A=πr^2=π(1.3r)^2=π(1.69r^2 )=1.69πr^2\)
\(1.69πr^2\) is \(69\%\) bigger than \(πr^2\).

Looking for the best resource to help you succeed on the ISEE Upper-Level Math test?

The Best Books to Ace the ISEE Upper Level Math Test