Full-Length ISEE Upper Level Math Practice Test

Taking a Full-length ISEE Upper-Level Math practice test is the best way to help you get familiar with the test format and feel more confident. Not only will this help you measure your exam readiness and solidify the concepts you’ve learned, but it is the best way to simulate test day.
To help you get the best out of this complete and realistic ISEE Upper-Level Math practice test and prepare your mind and body for the actual test, we recommend that you treat this practice test as a real test. Prepare scratch papers, a pencil, a timer, and a calculator and take the test in one sitting and follow the time limits to the minute.
Take the following full-length ISEE Upper-Level Math practice test to simulate the test day experience. After you’ve finished, score your tests using the answer keys.
Good luck!

The Absolute Best Book to Ace the ISEE Upper-Level Math Test

Time to refine your Math skill with a practice test

Take practice ISEE Upper-Level Math Tests to simulate the test day experience. After you’ve finished, score your tests using the answer keys.

Before You Start

• You’ll need a pencil, a calculator and a timer to take the test.
• For each question, there are four possible answers. Choose which one is best.
• It’s okay to guess. There is no penalty for wrong answers.
• Use the answer sheet provided to record your answers.
• After you’ve finished the test, review the answer key to see where you went wrong.

Good Luck!

Best ISEE Upper-Level Math Prep Resource for 2021

ISEE Upper-Level Math Practice Test

47 questions
Total time for this section: 40 Minutes
You may use a calculator for this test.

1- Solve. \(|15-(18÷|2-8|)|= \)?

A. \(8\)

B. \(-12\)

C. \(12\)

D. \(-8\)

2- \((x – 4) (2x + 2)\)=

A. \(2x^2 + 2x + 8\)

B.\(2x^2 – 4x – 8\)

C. \(2×2 + 8x + 12\)

D. \(2×2 -6x – 8\)

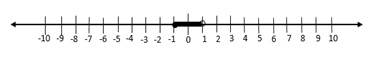
3- Which of the following graphs represents the compound inequality \( -4≤4x-5<7\)?

A.

B.

C.

D.

4- Find all values of x for which \(3x^2+8 x+4=0\)

A. \(-\frac{3}{2}, -\frac{1}{2}\)

B. \(–\frac{1}{2}, – 3\)

C. \(–2, –\frac{1}{3}\)

D. \(– \frac{2}{3}, -2\)

5- Which value of x makes the following inequality true? \(\frac{8}{23}≤ x < 45%\)

A. \(0.31\)

B. \(\frac{8}{19}\)

C. \(\sqrt{0.052}\)

D. \(0.512\)

6- Which graph shows a non-proportional linear relationship between \(x\) and \(y\)?

A.

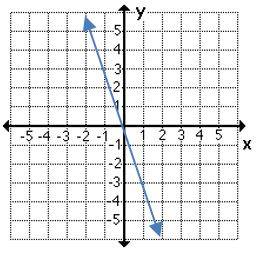
B.

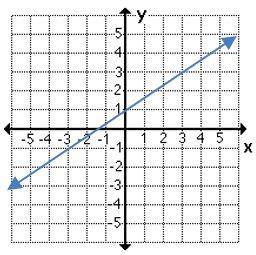
C.

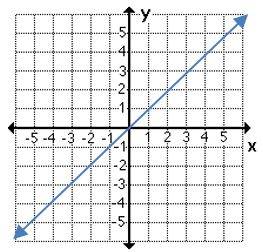
D.

7- The rectangle on the coordinate grid is translated 6 units down and 5 units to the left.
Which of the following describes this transformation?

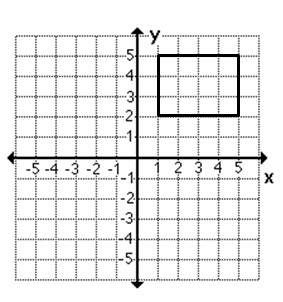
A. \((x,y) ⇒ (x-6,y-5)\)

B. \((x,y) ⇒ (x-6,y+5)\)

C. \((x,y) ⇒ (x+5,y+6)\)

D. \((x,y) ⇒ (x-5,y-6)\)

8- A girl 150 cm tall, stands 280 cm from a lamp post at night. Her shadow from the light is 100 cm long. How high is the lamp post?

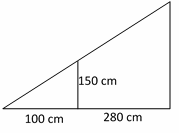
A. 550

B. 570

C. 590

D. 600

9- How is this number written in scientific notation? 0.00000625

A. \(6.25 × 10^{-8}\)

B. \(6.25 × 10^{-6}\)

C. \(0.625 × 10^{-7}\)

D. \(62.5 × 10^{-8}\)

10- The ratio of boys to girls in a school is 7:5. If there are 540 students in a school, how many boys are in the school?

A. 285

B. 315

C. 345

D. 385

11- There are 5 blue marbles, 7 red marbles, and 6 yellow marbles in a box. If Ava randomly selects a marble from the box, what is the probability of selecting a red or yellow marble?

A. \(\frac{7}{13}\)

B. \(\frac{1}{3}\)

C. \(\frac{13}{18}\)

D. \(\frac{18}{13}\)

12- Emily and Daniel have taken the same number of photos on their school trip. Emily has taken 9 times as many photos as Claire and Daniel has taken 24 more photos than Claire. How many photos has Claire taken?

A. 3

B. 4

C. 6

D. 10

13- Emily lives \(4 \frac{2}{5}\) miles from where she works. When traveling to work, she walks to a bus stop \(\frac{1}{4}\) of the way to catch a bus. How many miles away from her house is the bus stop?

A. \(1 \frac{1}{3} Miles\)

B. \(1 \frac{1}{10} Miles\)

C. \(1 \frac{3}{10} Miles\)

D. \(1 \frac{3}{5} Miles\)

14- Use the diagram below to answer the question.
Given the lengths of the base and diagonal of the rectangle below, what is the length of height h, in terms of s?

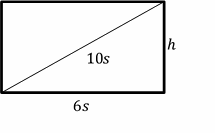
A. \(8s\sqrt{2}\)

B. \(4s\sqrt{7}\)

C. \(5s\)

D. \(8s\)

15- \(5 – 12 ÷ (2^4 ÷ 4) =?\)

A. \(-3\)

B. \(\frac{3}{4}\)

C. \(2\)

D. \(3\)

16- If the area of a trapezoid is 36 cm, what is the perimeter of the trapezoid?

A. 12 cm

B. 22 cm

C. 32 cm

D. 42 cm

17- If a vehicle is driven 40 miles on Monday, 30 miles on Tuesday, and 38 miles on Wednesday, what is the average number of miles driven each day?

A. 29 Miles

B. 31 Miles

C. 32 Miles

D. 36 Miles

18- Find the area of a rectangle with a length of 212 feet and a width of 52 feet.

A. 12,296sq. ft

B. 12,521sq. ft

C. 12,396sq. ft

D. 12,855sq. ft

19- If \((6.2+6.3+6.5) x = x+2\), then what is the value of \(x\)?

A. \(0\)

B. \(\frac{1}{9}\)

C. \(1\)

D. \(10\)

20- With an \(16\%\) discount, Ella was able to save \($15.4\) on a dress. What was the original price of the dress?

A. $94.56

B. $95.62

C. $96.25

D. $98.52

21- \(\frac{9}{30}\) is equals to:

A. 0.03

B. 0.27

C. 0. 29

D. 0.3

22- The sum of 8 numbers is greater than 240 and less than 320. Which of the following could be the average (arithmetic mean) of the numbers?

A. 30

B. 35

C. 40

D. 45

23- \(75 ÷ \frac{1}{6}=?\)

A. 12.5

B. 80

C. 230

D. 450

24- Two dice are thrown simultaneously, what is the probability of getting a sum of 5 or 7?

A. \(\frac{1}{3}\)

B. \(\frac{1}{4}\)

C. \(\frac{1}{6}\)

D. \(\frac{5}{18}\)

25- Simplify \(\frac{\frac{1}{4}-\frac{x-7}{8}}{\frac{x^2}{4}-\frac{1}{4}}\)

A. \(\frac{3 – x}{x^2 – 2}\)

B. \(\frac{-9 – x}{2x^2 – 2}\)

C. \(\frac{x+5}{2x^2 – 2}\)

D. \(\frac{-x – 5}{2x^2 – 2}\)

26- In the following figure, AB is the diameter of the circle. What is the circumference of the circle?

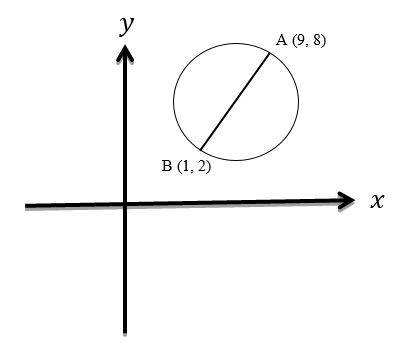
A. 5\(π\)

B. 8\(π\)

C. 10\(π\)

D. 12\(π\)

27- \(102.5÷0.55 =?\)

A. 18.652

B. 186.36

C. 186.85

D. 188.36

28- A circle has a diameter of 14 inches. What is its approximate area?

A. 120.56

B. 125.5

C. 153.86

D. 200.96

29- If 15 garbage trucks can collect the trash of 45 homes in a day. How many trucks are needed to collect in 120 houses?

A. 12

B. 15

C. 30

D. 40

30- Solve for \(4x^2 -34 = 66\)

A. \(±\) 3

B. \(±\) 5

C. \(±\) 9

D. \(±\) 10

Use the following table to answer the question below.

31- This table shows the data Daniel collects while watching birds for one week. How many raptors did Daniel see on Monday?

A. 5

B. 8

C. 12

D. 13

32- A floppy disk shows 856,036 bytes free and 739,352 bytes used. If you delete a file of size 652,159 bytes and create a new file of size 599,986 bytes, how many free bytes will the floppy disk have?

A. 114,857

B. 123.986

C. 221,867

D. 302,209

33- 6 days 14 hours 42 minutes – 4 days 12 hours 35 minutes =?

A. 2 days 1 hours 10 minutes

B. 2 days 2 hours 7 minutes

C. 2 days 2 hours 13 minutes

D. 2 days 7 hours 23 minutes

34- If \(15+x^{\frac{1}{2}}=24\), then what is the value of \(8 × x\)?

A. 321

B. 456

C. 550

D. 648

35- Increased by \(35\%\), the numbers \(60\) becomes:

A. 42

B. 56

C. 75

D. 81

36- Which equation represents the statement twice the difference between 8 times h and 4 gives 42.

A. \(\frac{8H + 4}{2} = 42\)

B. \(2(8H + 4) = 42\)

C. \(2(8H – 4) = 42\)

D. \(4 \frac{8H}{2} = 42\)

37- A circle is inscribed in a square, as shown below.
The area of the circle is \(64π \space cm^2\). What is the area of the square?

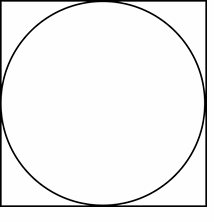
A. \(64π \space cm^2\)

B. \(121π \space cm^2\)

C. \(144π \space cm^2\)

D. \(256π \space cm^2\)

38- The base of a right triangle is 4 feet, and the interior angles are 45-45-90. What is its area?

A. 6 square feet

B. 7 square feet

C. 8 square feet

D. 10 square feet

39- Triangle ABC is graphed on a coordinate grid with vertices at A \((-2, -2)\), B \((-3, 8)\) and C \((5, 4)\). Triangle ABC is reflected over axes to create triangle A’B’C’.
Which order pair represents the coordinate of C’?

A. \((-5, -4)\)

B. \((5, 4)\)

C. \((5, -4)\)

D. \( (-5, 4)\)

40- Which set of ordered pairs represents y as a function of \(x\)?

A. \({(2, 8), (3, 7), (9, -8), (4, -7)}\)

B. \({(4, 2), (3, -9), (5, 8), (4, 7)}\)

C. \({(9, 12), (5, 7), (6, 11), (5, 18)}\)

D. \({(6, 1), (6, 3), (0, 5), (4, 5)}\)

41- The width of a box is one-fourth of its length. The height of the box is one-third of its width. If the length of the box is 24 cm, what is the volume of the box?

A. \(81 \space cm^3\)

B. \(162 \space cm^3\)

C. \(252 \space cm^3\)

D. \(288 \space cm^3\)

42- A square measures 8 inches on one side. By how much will the area be decreased if its length is increased by 4 inches and its width increased by 2 inches.

A. 5 sq increased

B. 6 sq increased

C. 8 sq increased

D. 9 sq increased

43- If a box contains red and blue balls in a ratio of 3: 5 red to blue, how many red balls are there if 120 blue balls are in the box?

A. 48

B. 72

C. 84

D. 85

44- How many 5 × 5 squares can fit inside a rectangle with a height of 42 and a width of 20?

A. 33

B. 35

C. 37

D. 42

45- David makes a weekly salary of \($250\) plus \(12\%\) commission on his sales. What will his income be for a week in which he makes sales totaling \($1,800\)?

A. $328

B. $452

C. $466

D. $485

46- \(5x^3 y^4+14x^2 y-(3x^3 y^4-3x^2 y)=\)

A. \(8x^3 y^4+17x^2 y\)

B. \(2x^3 y^4+11x^2 y\)

C. \(2x^3 y^4-17x^2 y\)

D. \(2x^3 y^4+17x^2 y\)

47- The radius of circle A is fifth times the radius of circle B. If the circumference of circle A is 20π, what is the area of circle B?

A. 3π

B. 4π

C. 9π

D. 12π

The Best Books to Ace the ISEE Upper-Level Math Test

Answers and Explanations