How to Scale a Function Horizontally?
Horizontal scaling means stretching or shrinking the diagram of function along the \(x\)-axis. In the following guide, you will learn how to horizontal scaling.
[include_netrun_products_block from-products="product/6-south-carolina-sc-ready-grade-3-math-practice-tests/" product-list-class="bundle-products float-left" product-item-class="float-left" product-item-image-container-class="p-0 float-left" product-item-image-container-size="col-2" product-item-image-container-custom-style="" product-item-container-size="" product-item-add-to-cart-class="btn-accent btn-purchase-ajax" product-item-button-custom-url="{url}/?ajax-add-to-cart={id}" product-item-button-custom-url-if-not-salable="{productUrl} product-item-container-class="" product-item-element-order="image,title,purchase,price" product-item-title-size="" product-item-title-wrapper-size="col-10" product-item-title-tag="h3" product-item-title-class="mt-0" product-item-title-wrapper-class="float-left pr-0" product-item-price-size="" product-item-purchase-size="" product-item-purchase-wrapper-size="" product-item-price-wrapper-class="pr-0 float-left" product-item-price-wrapper-size="col-10" product-item-read-more-text="" product-item-add-to-cart-text="" product-item-add-to-cart-custom-attribute="title='Purchase this book with single click'" product-item-thumbnail-size="290-380" show-details="false" show-excerpt="false" paginate="false" lazy-load="true"]
Horizontal scaling refers to the shrinking or stretching of the curve along the \(x\)-axis by some specific units.
Related Topics
A step-by-step guide to horizontal scaling
Horizontal scaling means stretching or shrinking the diagram of function along the \(x\)-axis. The horizontal scale can be done by multiplying the input by a constant.
Consider the following example:
If we have a function,\(y=f(x)\), the horizontal scaling of this function can be written as: \(y=f(Cx)\).
Note:
- If \(C>1\), the graph shrinks.
- If \(C<1\), the graph stretches.
How is a graph scaled horizontally?
- Step 1: Select a constant with which we want to scale the function.
- Step 2: Write the new function as \(g(x)=fC(x)\), where \(C\) is the constant.
- Step 3: Trace the new function graph by replacing each value of \(x\) with \(Cx\).
- Step 4: \(X\) coordinate of each point in the graph is multiplied by \(±C\), and the curve shrinks or stretches accordingly.
Original price was: $109.99.$54.99Current price is: $54.99.
Horizontal Scaling – Example 1:
Horizontally stretch the function \(f(x)=x+2\) by a factor of \(2\) units.
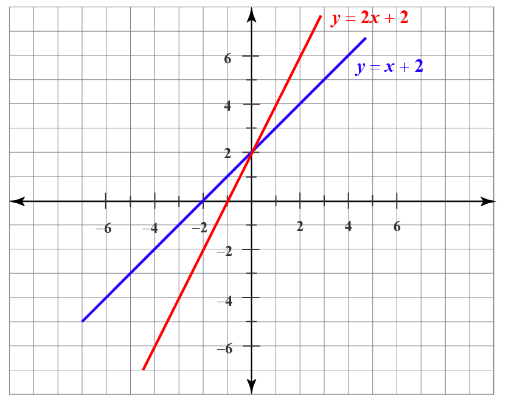
Exercises for Horizontal Scaling
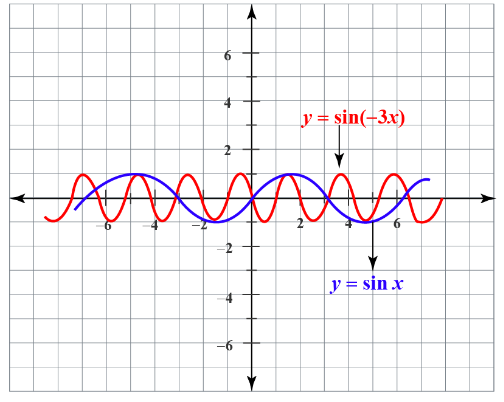
- Horizontal scaling of function \(f(x) = sin x\) by a factor of \(-3\).
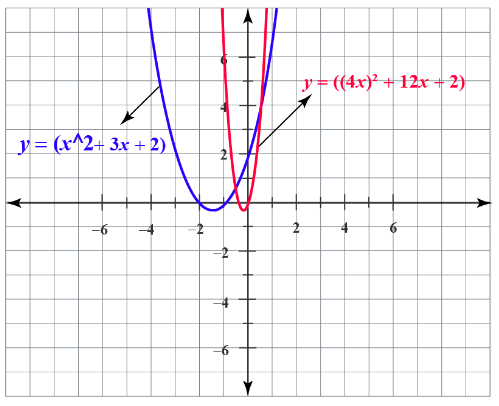
- Horizontal scaling of function \(f(x) =x^2+3x+2\) by a factor of \(4\).
Original price was: $109.99.$54.99Current price is: $54.99.
Related to This Article
More math articles
- The Ultimate ATI TEAS 7 Math Formula Cheat Sheet
- The Ultimate Trigonometry Course (+FREE Worksheets)
- A Comprehensive Collection of Free CBEST Math Practice Tests
- Everything You Need to Know to Pass Algebra 1
- Word Problems of Comparing and Ordering Rational Numbers
- Volume Calculation Method of Cross-Sections
- How to Get ALEKS Done Fast?
- 10 Most Common 8th Grade FSA Math Questions
- How to Solve Triangles Problems? (+FREE Worksheet!)
- How to Find the Surface Area of Spheres?
What people say about "How to Scale a Function Horizontally? - Effortless Math: We Help Students Learn to LOVE Mathematics"?
No one replied yet.