HiSET Math FREE Sample Practice Questions

Preparing for the HiSET Math test? To do your best on the HiSET Math test, you need to review and practice real HiSET Math questions.  There’s nothing like working on HiSET Math sample questions to hone your math skills and put you more at ease when taking the HiSET Math test.

The sample math questions you’ll find here are brief samples designed to give you the insights you need to be as prepared as possible for your HiSET Math test.

Check out our sample HiSET Math practice questions to find out what areas you need to practice more before taking the HiSET Math test!

Start preparing for the 2022 HiSET Math test with our free sample practice questions. Also, make sure to follow some of the related links at the bottom of this post to get a better idea of what kind of mathematics questions you need to practice.

The Absolute Best Book to Ace the HiSET Math Test

10 Sample HiSET Math Practice Questions

1- What is the median of these numbers? \(4, 9, 13, 8, 15, 18, 5\)

A. 8

B. 9

C. 13

D. 15

E. 20

2- The radius of the following cylinder is 8 inches and its height is 12 inches. What is the surface area of the cylinder?

A. \(64 \space π \space in^2\)

B. \(128 \space π \space in^2\)

C. \(192 \space π \space in^2\)

D. \(256 \space π \space in^2\)

E. \(320 \space π \space in^2\)

3- The average of \(13, 15, 20\) and \(x\) is \(18\). What is the value of \(x\)?

A. 9

B. 15

C. 18

D. 20

E. 24

4- The price of a sofa is decreased by \(25\%\) to \(\$420\). What was its original price?

A. $480

B. $520

C. $560

D. $600

E. $800

5- What are the zeros of the function: \(f(x)=x^3+5x^2+6x?\)

A. 0

B. \(– 2, – 3\)

C. \(0, 2, 3\)

D.\( – 1, – 3\)

E. \(0, – 2, – 3\)

6- A bank is offering \(4.5\%\) simple interest on a savings account. If you deposit \(\$8,000\), how much interest will you earn in five years?

A. $360

B. $720

C. $1800

D. $3600

E. $4800

7- Multiply and write the product in scientific notation:
\((3.2 × 10^6) × (2.6 × 10^{−5})\)

A. \(832 × 10\)

B. \(83.2 × 10^6\)

C. \(83.2 × 10^{−5}\)

D. \(8.32 × 10^{11}\)

E. \(8.32 × 10\)

8- If the height of a right pyramid is \(12 cm\) and its base is a square with a side of \(6 cm\). What is its volume?

A. \(432 cm^3\)

B. \(108 cm^3\)

C. \(36 cm^3\)

D. \(72 cm^3\)

E. \(144 cm^3\)

9- In a coordinate plane, triangle ABC has coordinates: \((−1,6)\), \((−2,5)\), and \((5,8)\). If triangle ABC is reflected over the \(y\)-axis, what are the coordinates of the new image?

A. \((−1, −6), (−2, −5), (−5, −8)\)

B. \((−1, −6), (−2, −5), (5, −8)\)

C. \((1, 6), (2, 5), (5, 8)\)

D. \((−1, 6), (−2, 5), (5, 8)\)

E. \((1, 6), (2, 5), (−5, 8)\)

10- Calculate the value of \(x\) for the right triangle shown below.

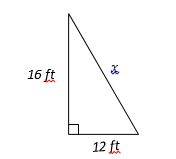
A. 6 ft

B. 12 ft

C. 16 ft

D. 18 ft

E. 20 ft

Best HiSET Math Prep Resource for 2022

Answers:

2- E
Surface Area of a cylinder \(= 2πr (r + h)\),
The radius of the cylinder is 8 inches and its height is 12 inches.
Surface Area of a cylinder \(= 2 (π) (8) (8 + 12) = 320 π\)

3- E
\(average = \frac{sum of terms}{number of terms}\)
\(18 = \frac{13+15+20+x}{4}\)
\(72 = 48 + x ⇒ x = 24\)

4- C
Let \(x\) be the original price.
If the price of the sofa is decreased by \(25\%\) to \(\$420\), then: \(75 \%\) of \(x=420 ⇒ 0.75x=420 ⇒ x=420÷0.75=560\)

5- E
Frist, factor the function:
\(x (x+2)(x+3)\)
To find the zeros, \(f(x)\) should be zero.
\(f(x)=x (x+2)(x+3)=0\)
Therefore, the zeros are:
\(x=0\)
\((x+2)=0 ⇒ x= -2\)
\((x+3)=0 ⇒ x= -3\)

The Best Quick Study Guide for the HiSET Math Test

6- C
Use simple interest formula:
\(I=prt\)
(I = interest, p = principal, r = rate, t = time)
\(I=(8,000)(0.045)(5)=1,800\)

7- E
\((3.2 × 10^6) × (2.6 × 10^{−5}) = (3.2 × 2.6) × (10^6 × 10^{−5}) = 8.32 × (10^{6 + (−5)} ) = 8.32 × 10^1\)

8- E
The formula of the volume of the pyramid is:
\(V=\frac{l ×w ×h}{3}\)
\(V=\frac{6×6 ×12}=144 cm^3\)

9- E
the triangle ABC is reflected over the \(y\)-axis, then all values of \(y\)’s of the points don’t change and the sign of all \(x\)’s change.
(remember that when a point is reflected over the \(y\)-axis, the value of \(y\) does not change and when a point is reflected over the \(x\)-axis, the value of \(x\) does not change).
Therefore:
\((−1,6)\) changes to \((1, 6)\)
\((−2, 5)\) changes to \((2, 5)\)
\((5, 8)\) changes to \((−5, 8)\)

10- E
Use Pythagorean theorem:
\(a^2 + b^2 = c^2\)
\(12^2 + 16^2 = x^2\)
\(144 + 256 = x^2\)
\(400 = x^2\)
\(x = 20\)

High School Equivalency Tests

The Best Books to Ace the HiSET Math Test